Determining the resistivity of intrinsic Germanium

[jisbon]

Homework Statement

At room temperature (300 K), the bandgap energy and resistivity of
intrinsic germanium is 0.67 eV and 0.455 ohm/m, respectively.
Determine the resistivity of the intrinsic germanium at 150 °C. Assume
that, at room temperature, the electron and hole mobilities are 0.14 and
0.05, respectively. The bandgap is insensitive to the temperature.

Relevant Equations

Shown below.

Hi.
Since,

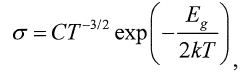
I can find conductivity by taking the reciprocal of resistivity, in this case, 1/0.455
Hence, I will end up with:
$\frac{1}{0.455}=C(300)^{-3/2}e^{(\frac{-0.67}{2(1.38*10^{-23})(300)})}$
However, my C value seems to be invalid in this case.
May I know what may went wrong here? Thanks

 

[Dr Transport]

take the ratio of the conductivities at the two twmperatures and the constant will drop out...

 

[jisbon]

take the ratio of the conductivities at the two twmperatures and the constant will drop out...

The ratio seems to be undefined too:

 

[Dr Transport]

look at the magnitude of your exponent...

 

[ZapperZ]

Not only that, but you should really do the ratio algebraically first before plugging in all those numbers. Give σ and T different subscripts, while everything else is common to both.

It is easier to deal with, and it is why we try to teach the students to do at the General Physics level.

Zz.

 

[jisbon]

look at the magnitude of your exponent...

The formula states that it has a negative sign though. Is the formula wrong in this case..? Sorry

 

[Dr Transport]

The formula states that it has a negative sign though. Is the formula wrong in this case..? Sorry

\approx 10^{23}

 

[jisbon]

Isn't the Boltzmann constant 10 to the power of - 23?

\approx 10^{23}

 

[Dr Transport]

check your units, you're missing something

 

[Dr Transport]

your Boltzmann constant is in JK^{-1} and your band gap is in eV.