Difference of angles in a triangle

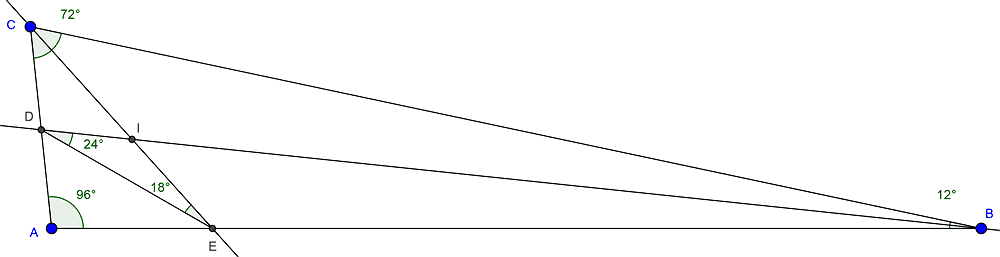
In summary, the conversation discusses a problem involving a triangle ABC and its bisectors, D and E. The measures of angles BDE and CED are given, and the task is to find the difference in degrees between the two smallest angles of the triangle. It is suggested to use the properties of intersecting lines and angle bisectors, as well as the fact that triangle angles add up to 180 degrees, to solve the problem without relying on Geogebra. The Angle Bisector Theorem is mentioned as a potential tool for solving the problem.
  • #1
maxkor
84
0
In a triangle ABC, let D and E be the intersections of the bisectors of the angles ABC and ACB with the sides AC and AB, respectively. Knowing that the measures in degrees of the angles BDE and CED are equal to 24 and 18, respectively, calculate the difference in degrees between the measures of the two smallest angles of the triangle. CAB angle = 96 degrees.

I checked with Geogebra:
Geogebra online(7).png

But how to solve this problem without Geogebra?
 
Mathematics news on Phys.org
  • #2
Recalling that plane Euclidean triangle angles add up to 180 degrees, opposite angles in intersecting lines are equal and angle bisectors split angles in half, we can use inspection to determine all the angles in the diagram.

As an example, by inspection, triangle DEI has two angles shown so we can compute the missing angle EID as 180-24-18 = 138 degrees.
 
  • Like
Likes Greg Bernhardt
  • #3
so how to calculate for example angle ABC?
 

FAQ: Difference of angles in a triangle

What is the difference of angles in a triangle?

The difference of angles in a triangle refers to the difference between the largest angle and the smallest angle in the triangle. It is also known as the angle sum property, which states that the sum of all angles in a triangle is always equal to 180 degrees.

How can I find the difference of angles in a triangle?

To find the difference of angles in a triangle, you can subtract the smallest angle from the largest angle. For example, if the largest angle is 90 degrees and the smallest angle is 30 degrees, the difference would be 60 degrees.

Is the difference of angles in a triangle always the same?

No, the difference of angles in a triangle can vary depending on the size and shape of the triangle. However, the sum of all angles in a triangle will always be 180 degrees.

Why is the difference of angles in a triangle important?

The difference of angles in a triangle is important because it helps us identify the type of triangle. For example, if the difference is 0 degrees, then the triangle is equilateral. If the difference is 90 degrees, then the triangle is right-angled. It also helps us understand the relationship between the angles in a triangle.

Can the difference of angles in a triangle be negative?

No, the difference of angles in a triangle cannot be negative. It is always measured as a positive value, as it represents the difference between two angles. If the difference is negative, it means that the angles were not measured correctly or that the triangle is not a valid triangle.

Similar threads

MHB Find $\angle B$ for Triangle $ABC$ with Bisectors $AD,BE$
Replies
1
Views
969
MHB Find ∠A & ∠C in Triangle Geometry
Replies
1
Views
2K
B A triangle problem: Prove that |AC|+|AB|=|PR|+|PQ| given some constraints
Replies
13
Views
2K
MHB Proving Equality of Angles in an Acute Triangle
Replies
4
Views
971
MHB What are the angles of an isosceles triangle with a specific ratio?
Replies
2
Views
1K
MHB What are the angles of isosceles triangle ABC?
Replies
1
Views
972
MHB Can You Find the Angle in This Isosceles Triangle Problem?
Replies
1
Views
1K
MHB Find Length of Side in Right Triangle w/ 45°, 90°, and 45° Angle
Replies
2
Views
1K
MHB Could you help me set up these geometric problems?
Replies
2
Views
3K
MHB What is the smallest side length BC of triangle ABC with fixed angle and area?
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top