- #1
maxkor
- 84
- 0
In a triangle ABC, let D and E be the intersections of the bisectors of the angles ABC and ACB with the sides AC and AB, respectively. Knowing that the measures in degrees of the angles BDE and CED are equal to 24 and 18, respectively, calculate the difference in degrees between the measures of the two smallest angles of the triangle. CAB angle = 96 degrees.
I checked with Geogebra:
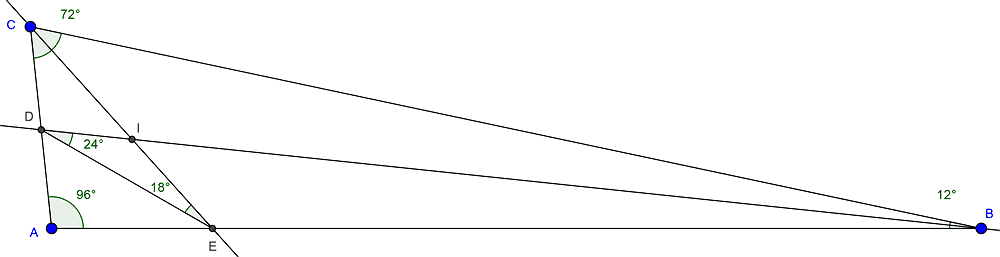
But how to solve this problem without Geogebra?
I checked with Geogebra:
But how to solve this problem without Geogebra?