MHB Difference of angles in a triangle

Click For Summary
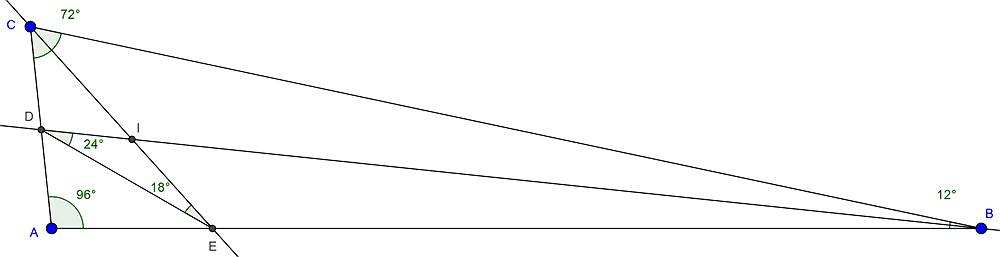
SUMMARY

The discussion centers on calculating the difference between the two smallest angles in triangle ABC, where angle CAB measures 96 degrees, and angles BDE and CED measure 24 and 18 degrees, respectively. Utilizing the properties of angle bisectors and the fact that the sum of angles in a triangle equals 180 degrees, participants derive that angle EID is 138 degrees. The angle bisector theorem is referenced as a potential method for further calculations, emphasizing the importance of understanding angle relationships in triangle geometry.

PREREQUISITES
  • Understanding of triangle properties, specifically the sum of angles in a triangle.
  • Familiarity with angle bisectors and their properties.
  • Basic knowledge of Euclidean geometry.
  • Ability to perform angle calculations and deductions.
NEXT STEPS
  • Study the Angle Bisector Theorem in detail.
  • Practice solving triangle angle problems using Geogebra.
  • Learn how to apply the Law of Sines in triangle calculations.
  • Explore advanced triangle properties, including the relationship between angles and side lengths.
USEFUL FOR

Students of geometry, mathematics educators, and anyone interested in solving triangle-related problems without relying on software tools like Geogebra.

maxkor
Messages
79
Reaction score
0
In a triangle ABC, let D and E be the intersections of the bisectors of the angles ABC and ACB with the sides AC and AB, respectively. Knowing that the measures in degrees of the angles BDE and CED are equal to 24 and 18, respectively, calculate the difference in degrees between the measures of the two smallest angles of the triangle. CAB angle = 96 degrees.

I checked with Geogebra:
Geogebra online(7).png

But how to solve this problem without Geogebra?
 
Mathematics news on Phys.org
Recalling that plane Euclidean triangle angles add up to 180 degrees, opposite angles in intersecting lines are equal and angle bisectors split angles in half, we can use inspection to determine all the angles in the diagram.

As an example, by inspection, triangle DEI has two angles shown so we can compute the missing angle EID as 180-24-18 = 138 degrees.
 
Reply
  • Like
Likes Greg Bernhardt
so how to calculate for example angle ABC?
 

Similar threads

MHB Find ∠A & ∠C in Triangle Geometry
  • · Replies 1 ·
Replies
1
Views
2K
High School A triangle problem: Prove that |AC|+|AB|=|PR|+|PQ| given some constraints
  • · Replies 13 ·
Replies
13
Views
3K
MHB Proving Equality of Angles in an Acute Triangle
  • · Replies 4 ·
Replies
4
Views
1K
MHB What are the angles of an isosceles triangle with a specific ratio?
  • · Replies 2 ·
Replies
2
Views
1K
MHB Can You Find the Angle in This Isosceles Triangle Problem?
  • · Replies 1 ·
Replies
1
Views
1K
MHB Find Length of Side in Right Triangle w/ 45°, 90°, and 45° Angle
  • · Replies 2 ·
Replies
2
Views
2K
MHB Could you help me set up these geometric problems?
  • · Replies 2 ·
Replies
2
Views
3K
MHB What is the smallest side length BC of triangle ABC with fixed angle and area?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Act.ge.5 third angle of triangle
  • · Replies 1 ·
Replies
1
Views
1K
MHB Triangle ABC has area 25*sqrt(3). if Angle BAC=30 degrees, find |AC|=|BC|=?
  • · Replies 1 ·
Replies
1
Views
2K