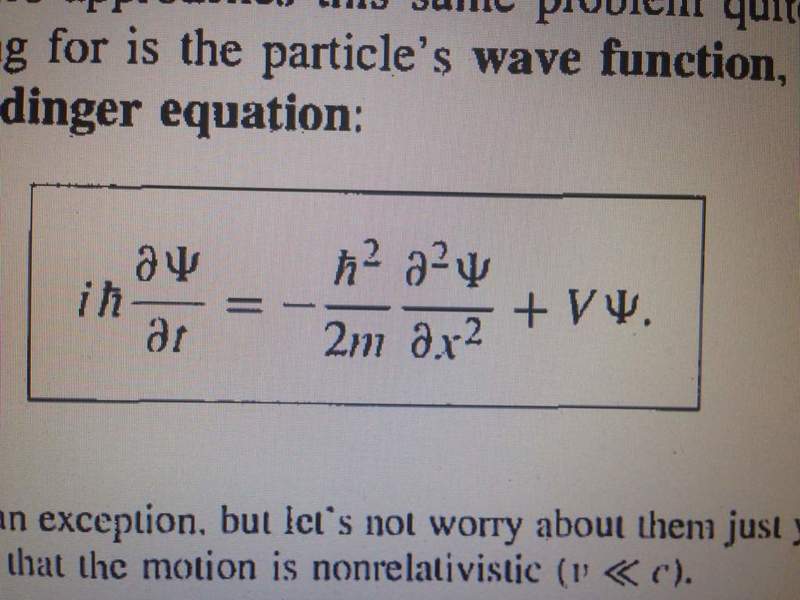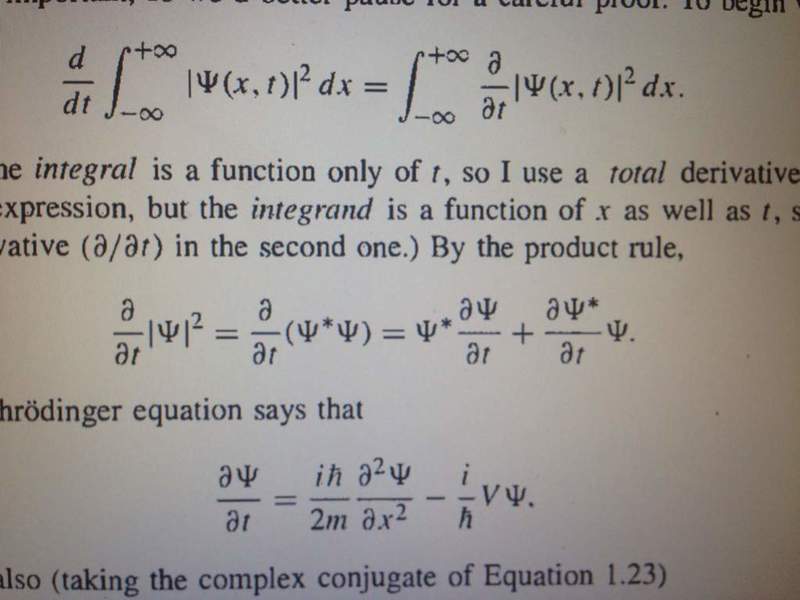SUMMARY
The discussion revolves around the transition between different forms of the Schrödinger equation in quantum mechanics. The user expresses confusion regarding the algebraic manipulation of the equations, particularly in relation to complex numbers. They highlight that the last equation in one representation is derived from another by multiplying by \(-\frac{i}{\hbar}\), clarifying the relationship between the two forms. This exchange emphasizes the importance of understanding complex number operations in quantum mechanics.
PREREQUISITES
- Understanding of the Schrödinger equation in quantum mechanics
- Familiarity with complex numbers and their properties
- Knowledge of algebraic manipulation techniques
- Basic grasp of quantum mechanics principles
NEXT STEPS
- Study the derivation of the time-dependent Schrödinger equation
- Learn about the role of complex numbers in quantum mechanics
- Explore the implications of the \(-\frac{i}{\hbar}\) factor in quantum equations
- Investigate different forms of the Schrödinger equation and their applications
USEFUL FOR
Students of quantum mechanics, physicists, and anyone seeking to deepen their understanding of the Schrödinger equation and complex number applications in physics.