SUMMARY
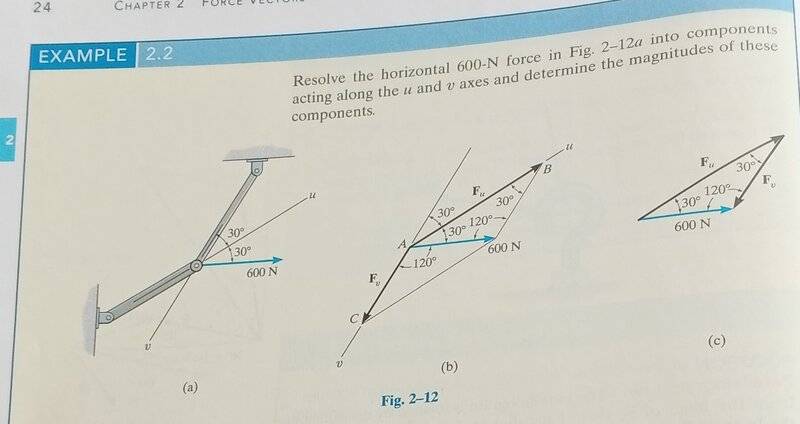
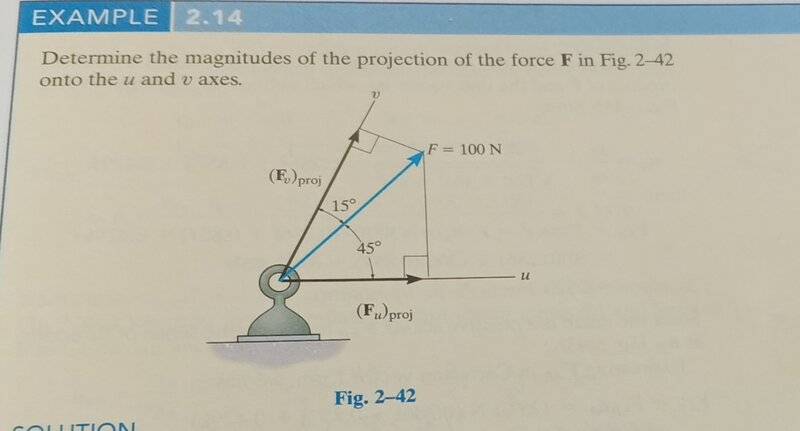
The discussion clarifies the distinction between resolving a vector into components and finding projections onto axes. Resolving a vector, such as ##\vec w##, into components ##\vec u## and ##\vec v## results in the equation ##\vec w = \vec u + \vec v##, where the components are only projections if ##\vec u## and ##\vec v## are orthogonal. In contrast, the projection of one vector onto another is solely dependent on those two vectors and remains unaffected by additional vectors. This difference is crucial for understanding vector decomposition in physics and engineering applications.
PREREQUISITES
- Understanding of vector notation and operations
- Familiarity with the dot product and its applications
- Knowledge of orthogonal vectors and their properties
- Basic concepts of vector resolution in physics
NEXT STEPS
- Study the properties of orthogonal vectors and their significance in vector resolution
- Learn about the geometric interpretation of the dot product in vector projections
- Explore applications of vector resolution in physics, particularly in mechanics
- Investigate advanced vector decomposition techniques in higher dimensions
USEFUL FOR
Students of physics, engineers, and anyone involved in vector analysis or mechanics who seeks to deepen their understanding of vector resolution and projections.