Direction Fields and Isoclines

[Kakashi]

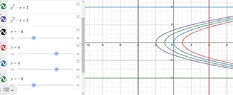
I sketched the isoclines for $$ m=-1,0,1,2 $$. Since both $$ \frac{dy}{dx} $$ and $$ D_{y} \frac{dy}{dx} $$ are continuous on the square region R defined by $$ -4\leq x \leq 4, -4 \leq y \leq 4 $$ the existence and uniqueness theorem guarantees that if we pick a point in the interior that lies on an isocline there will be a unique differentiable function (solution) passing through that point. I understand that a solution exists but I unsure how to actually sketch it. For example, consider a point (-2,0) which lies on the isocline $$ y^2-x=2 $$. At this point the slope is 2 so the differentiable function passing through it is increasing as x increases. How do I determine the approximate behavior of the solution curve for other points? How can I tell the solution will cross other isoclines and thus understand how the slope changes?

 

[Gavran]

How do I determine the approximate behavior of the solution curve for other points? How can I tell the solution will cross other isoclines and thus understand how the slope changes?

ODE | Slope fields and isoclines example