Direction of magnetic field and force in current wires

[Fluxxx]

I read this example in a book and I'm thinking about what is the "determining factor" of the directions of the magnetic field vector B and the magnetic force vectors F.

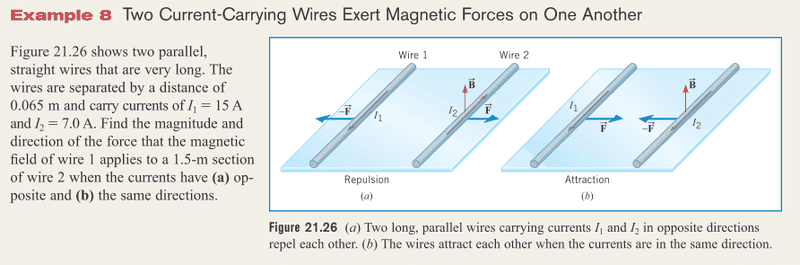
If we start by looking at wire 1 in picture (a), if we only know the direction of the current (we call this "v"), can we really say anything about the direction of F and B? I would say no. We need to know the directions at least two of the vectors v, B and F in order to find the direction of the third vector. Here we know v only. So which of the other, B or F, do we also know from the start? Is it in this case, determined simply Newtons third law, so that the two wires, will always direct their B and F so that the forces oppose each other? Is that the only thing which is "constant", so to speak?

If we compare (a) and (b) we can see that the magnetic field vector created in wire 1 must change direction, since the force vector changes direction but the current direction remains the same. So the B-vector in wire 1 in (b) must be directed downwards. But why does changing direction of the current in wire 2 change the direction of the magnetic field in wire 1? The only explanation I can find is that the directions of B and F in two wires are always directed in a way that Newtons third law holds.

Am I correct in concluding that Newtons third law is the "determining factor" of the directions of B and F?

 

[Orodruin]

If you know the direction of a current, then you know the direction of the field it generates. The field resulting in a force on conductor 2 is generated by the current in conductor 1 and vice versa. That the field is not shown at conductor 1 in the figure does not mean you cannot find out by applying the right-hand rule. (How do you think they deduced the direction of the field at conductor 2 in the first place?)

But also, yes, in magnetostatics the forces are a Newton action-reaction pair.

 

[Fluxxx]

If you know the direction of a current, then you know the direction of the field it generates. The field resulting in a force on conductor 2 is generated by the current in conductor 1 and vice versa. That the field is not shown at conductor 1 in the figure does not mean you cannot find out by applying the right-hand rule. (How do you think they deduced the direction of the field at conductor 2 in the first place?)

But also, yes, in magnetostatics the forces are a Newton action-reaction pair.

Of course I can find the field from the illustration, I was talking generally, you need two vectors to find the third.

So actually ignore the illustration, and just think of two parallel current-carrying wires next to each other. The only thing known is the direction of the currents. Is this enough information to find the directions of the B and F vectors?

 

[jtbell]

Magnetic field produced by a straight wire (e.g. your wire 1):

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magcur.html

Force exerted by a magnetic field (e.g. the field produced by your wire 1) on a straight wire (your wire 2):

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/forwir2.html

Putting them together - the magnetic force between two parallel wires:

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/wirfor.html

 

[Orodruin]

If you are given the currents you are given the very same information as the image gives you so I do not understand why you think it would make a difference to have the information on the currents instead of the image.

 

[Dale]

The only thing known is the direction of the currents. Is this enough information to find the directions of the B and F vectors?

Yes.

 

[Fluxxx]

So let's say you have two parallel wires with currents in opposite directions. If you have a force vector pointing downwards in the left wire, and the force pointing upwards in the right wire, then Newtons 3rd law would still hold. So how do you know how much of the force component from one wire is in the direction of the other wire?

 

[Orodruin]

You have to compute the magnetic field due to the other wire, this field will determine the force.

 

[jtbell]

So how do you know how much of the force component from one wire is in the direction of the other wire?

As Orodruin noted, you can calculate the directions of the fields and forces, given the geometry of the currents. Have you studied vector algebra yet, in particular the "cross product" of two vectors (as in e.g. $\vec F = I \vec l \times \vec B$)?

 

[Fluxxx]

Yes I know the cross product.

You have to compute the magnetic field due to the other wire, this field will determine the force.

But the magnetic field due to the other wire is not known. The only thing known is the direction of the currents, and that the wires are parallel. So how can you from only this info determine the directions?

 

[Dale]

So let's say you have two parallel wires with currents in opposite directions.

Then the force on each wire points away from the other wire.

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/wirfor.html

 

[Orodruin]

Yes I know the cross product.But the magnetic field due to the other wire is not known. The only thing known is the direction of the currents, and that the wires are parallel. So how can you from only this info determine the directions?

If you know the currents you can compute the fields. This is half the point of electromagnetism, computing how the currents influence the fields (the other point being how the fields influence the currents).

 

[Fluxxx]

Then the force on each wire points away from the other wire.

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/wirfor.html

Why do you write something that is already answered in the original post, and not even something I asked?

 

[Fluxxx]

If you know the currents you can compute the fields. This is half the point of electromagnetism, computing how the currents influence the fields (the other point being how the fields influence the currents).

Ok, but how do you compute them if you only know the current directions?

 

[Orodruin]

Ok, but how do you compute them if you only know the current directions?

Generally: You apply Maxwell's equation.
In this case the solution for a long straight conductor is already well known and you can also take that solution from memory if you remember it.

 

[Dale]

Why do you write something that is already answered in the original post, and not even something I asked?

Because you keep asking it. The answer doesn't change. If the currents are parallel then the force is attractive. If the currents are anti parallel then the force is repulsive. You can determine that using the cross product, as has been pointed out over and over.

If you don't want a repetitive answer then don't ask a repetitive question.

 

[Fluxxx]

Generally: You apply Maxwell's equation.
In this case the solution for a long straight conductor is already well known and you can also take that solution from memory if you remember it.

Maxwell's euqation? As far as I know there are four, so which one are you referring to?

Anyway maybe you can write what this "well known" solution is, that applies in this case?

 

[Dale]

Please read the hyperphysics links provided. They explain exactly how to determine the direction.

This thread is closed.