SUMMARY
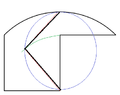
The discussion centers on the geometric division of a shape into two congruent pieces, specifically referencing a solution provided by a user named maxkor. The user utilizes TikZ, a LaTeX package for creating graphics, to illustrate the division. The focus is on achieving a perfect solution for dividing the shape, which was previously requested to be divided into five congruent pieces. The clarity of the solution demonstrates effective use of TikZ for geometric representation.
PREREQUISITES
- Understanding of geometric concepts related to congruence
- Familiarity with TikZ for LaTeX
- Basic knowledge of LaTeX document preparation
- Ability to interpret graphical representations in mathematics
NEXT STEPS
- Explore advanced TikZ techniques for complex geometric shapes
- Learn about congruence transformations in geometry
- Investigate LaTeX packages for enhanced graphical capabilities
- Study the principles of geometric proofs involving congruence
USEFUL FOR
Mathematicians, educators, and students interested in geometry, as well as LaTeX users looking to enhance their graphical representation skills.