- 16,335
- 258
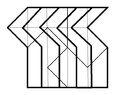
The following shows how a figure can be divided into 4 congruent pieces.
How can we divide the same figure into 5 congruent pieces?
\begin{tikzpicture}
\draw[ultra thick] (0,0) -- (4,0) -- (4,2) -- (3,3) -- (4,4) -- (0,4) -- (-1,3) -- (0,2) -- cycle;
\draw (0,2) -- (1,3) -- (2,2) -- (2,4);
\draw (4,2) -- (3,1) -- (2,2) -- (1,1) -- (2,0);
\end{tikzpicture}
How can we divide the same figure into 5 congruent pieces?
\begin{tikzpicture}
\draw[ultra thick] (0,0) -- (4,0) -- (4,2) -- (3,3) -- (4,4) -- (0,4) -- (-1,3) -- (0,2) -- cycle;
\draw (0,2) -- (1,3) -- (2,2) -- (2,4);
\draw (4,2) -- (3,1) -- (2,2) -- (1,1) -- (2,0);
\end{tikzpicture}