Vibhukanishk
- 2
- 0
What to say about this?
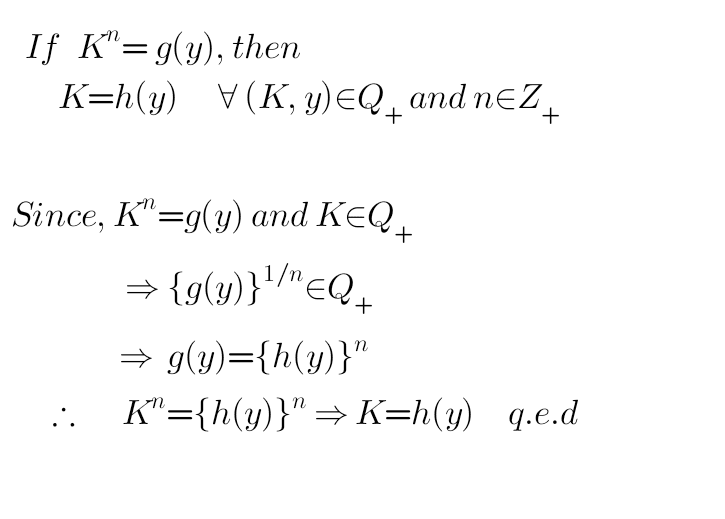
Is the logic used in the solution supports the statement?
Is the logic used in the solution supports the statement?
Does Defining ##g(y)## as ##h(y)^n## Validate the Statement?
- Context: Undergrad
- Thread starter Vibhukanishk
- Start date
-
- Tags
- Logic
Join the discussion
Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.
Real named experts · corrections over time · the nuance an AI answer skips
4 replies · 2K views
Gold Member
- 2,630
- 2,244
No. You just asserted that ##g(y)=h(y)^n## with no justification.
- 20,819
- 28,466
There is quite a bit of information missing. E.g., there is no quantifier on ##h(y)## in the initial statement.
Vibhukanishk
- 2
- 0
TeethWhitener said:
Gold Member
- 2,630
- 2,244
If you define ##g(y)## as ##h(y)^n##, then of course it's true, but there's also nothing to prove; it's all definitions.