Hello Duncan G,
1.) We are given the implicitly defined curve:
$$x^{\frac{1}{2}}+y^{\frac{1}{2}}=1$$
Implcitly differentiating with respect to $x$, we find:
$$\frac{1}{2}x^{-\frac{1}{2}}+\frac{1}{2}y^{-\frac{1}{2}}\frac{dy}{dx}=0$$
Solving for $$\frac{dy}{dx}$$, we obtain:
$$\frac{dy}{dx}=-\frac{y^{\frac{1}{2}}}{x^{\frac{1}{2}}}$$
Implicitly differentiating again with respect to $x$, we get:
$$\frac{d}{dx}\left(\frac{dy}{dx} \right)=-\frac{x^{\frac{1}{2}}\frac{1}{2}y^{-\frac{1}{2}}\frac{dy}{dx}-y^{\frac{1}{2}}\frac{1}{2}x^{-\frac{1}{2}}}{\left(x^{\frac{1}{2}} \right)^2}$$
Using the first derivative, and simplifying, we get:
$$\frac{d^2y}{dx^2}=\frac{1+\frac{y^{\frac{1}{2}}}{x^{\frac{1}{2}}}}{2x}$$
Multiplying by $$\frac{x^{\frac{1}{2}}}{x^{\frac{1}{2}}}$$, we have:
$$\frac{d^2y}{dx^2}=\frac{x^{\frac{1}{2}}+y^{\frac{1}{2}}}{2x^{\frac{3}{2}}}$$
Using the fact that $$x^{\frac{1}{2}}+y^{\frac{1}{2}}=1$$, we then get:
$$\frac{d^2y}{dx^2}=\frac{1}{2x^{\frac{3}{2}}}$$
We can check this result by explicitly differentiating. Let's write the original relation as:
$$y=\left(1-x^{\frac{1}{2}} \right)^2$$
$$\frac{dy}{dx}=2\left(1-x^{\frac{1}{2}} \right)\left(-\frac{1}{2}x^{-\frac{1}{2}} \right)=1-x^{-\frac{1}{2}}$$
$$\frac{d^2y}{dx^2}=\frac{1}{2}x^{-\frac{3}{2}}=\frac{1}{2x^{\frac{3}{2}}}$$
2.) We are given the implicit relation:
$$x^2y^2+xy=2$$
and asked to find the points where the slope of the tangent line is $-1$. So, implcitly differentiating with respect to $x$, we find:
$$x^2\cdot2y\frac{dy}{dx}+2xy^2+x\frac{dy}{dx}+y=0$$
Moving all terms not having $$\frac{dy}{dx}$$ as a factor to the right, we get:
$$x^2\cdot2y\frac{dy}{dx}+x\frac{dy}{dx}=-2xy^2-y$$
Factoring both sides:
$$\left(x(2xy+1) \right)\frac{dy}{dx}=-y(2xy+1)$$
Hence:
$$\frac{dy}{dx}=-\frac{y}{x}$$
Equating this slope to $-1$, we obtain:
$$y=x$$
Substituting for $y$ in the original equation, and writing in standard form, we may solve for $x$:
$$x^4+x^2-2=0$$
Factor:
$$\left(x^2+2 \right)\left(x^2-1 \right)=0$$
The first factor has imaginary roots, so we are left with:
$$x=\pm1$$
Now, since $y=x$, the two points are then:
$$(-1,-1),\,(1,1)$$
Here is a plot of the curve ant its two tangent lines with slope $-1$:
View attachment 1501
3.) Let's orient our coordinate axes such that ship A is at the origin at noon, and so ship B is at $(150,0)$. Thus, we may describe the position of each ship parametrically as follows:
Ship A:
$$x=35t$$
$$y=0$$
Ship B:
$$x=150$$
$$y=25t$$
If we let $D$ be the distance between the ships at time $t$, we may use the distance formula to write:
$$D^2(t)=(35t-150)^2+(25t)^2=50\left(37t^2-210t+450 \right)$$
Implicitly differentiating with respect to $t$, we find:
$$2D(t)D'(t)=50(74t-210)=100(37t-105)$$
Hence:
$$D'(t)=\frac{50(37t-105)}{D(t)}=\frac{\sqrt{50}(37t-105)}{\sqrt{37t^2-210t+450}}$$
At 4:00 pm, we have $t=4$, and so we find:
$$D'(4)=\frac{\sqrt{50}(37(4)-105)}{\sqrt{37(4)^2-210(4)+450}}=\frac{215}{\sqrt{101}}\,\frac{\text{km}}{\text{hr}}$$
Thus, at 4:00 pm the distance between the ships is increasing at a rate of about 21.3933 kph.
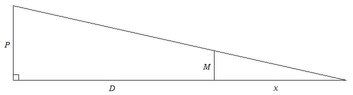
4.) Please refer to the following diagram:
View attachment 1502
$P$ is the height of the pole, $M$ is the height of the man, $D$ is the man's distance from the pole, and $x$ is the length of the shadow.
By similarity, we find:
$$\frac{D+x}{P}=\frac{x}{M}$$
$$DM+Mx=Px$$
$$x=\frac{DM}{P-M}$$
Observing that $x$ and $D$ are changing with time, we find by implcitly differentiating with respect to time $t$, we have:
$$\frac{dx}{dt}=\frac{M}{P-M}\frac{dD}{dt}$$
Also observing that movement of the tip of the man's shadow is the result not only of the shadow growing but also of the man's movement, we find that we must add these rates of change, so that the rate of change of the point $T$ of the tip of the shadow is given by:
$$\frac{dT}{dt}=\frac{dD}{dt}+\frac{dx}{dt}=\frac{dD}{dt}\left(1+\frac{M}{P-M} \right)=\frac{P}{P-M}\frac{dD}{dt}$$
Now, using the given data (did you notice we do not need $D$?):
$$P=15\text{ ft},\,M=6\text{ ft},\,\frac{dD}{dt}=5\,\frac{\text{ft}}{\text{s}}$$
We find:
$$\frac{dT}{dt}=\frac{15}{15-6}\cdot5\,\frac{\text{ft}}{\text{s}}=\frac{25}{3}\,\frac{\text{ft}}{\text{s}}$$