kurt101
- 285
- 35
- TL;DR
- Does inserting an analyzer loop in the EPR experiment with photons affect the non-local correlation in this experiment?
Given an EPR experiment such as the Alain Aspect 1982 test of non-locality using photons; if you modified the experiment so that the entangled photons first go through a analyzer loop (polarizer + inverse polarizer) before going to the polarizers in the experiment would you still see a non-local correlation between the entangled photons in this experiment?
A loop analyzer is a polarizer and its inverse polarizer that does not change the polarization as show in the following diagram:
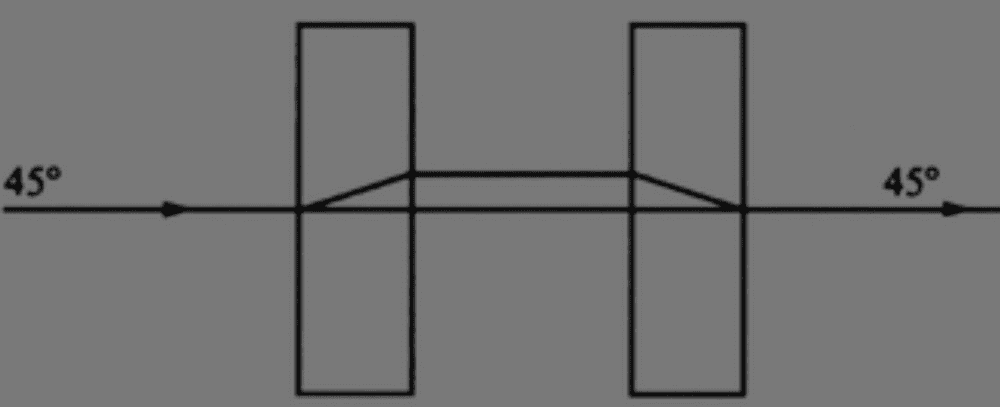
A loop analyzer is a polarizer and its inverse polarizer that does not change the polarization as show in the following diagram: