Hubabuh
- 1
- 0
For a day and a half now we have been trying to calculate a self-assigned problem. However, this has not turned out to be easy and build-up frustration has lead us to this forum. Our challenge was to calculate what under pressure a food packing company needs in it's jars to make sure the lid snaps inside after packing.
Schematically represented is the intersection in the following figure:
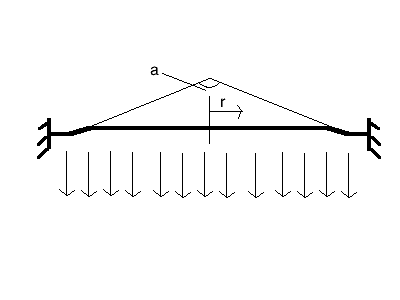
This is not a difficult exercise if this was just a beam construction. This is however a difficult exercise if it is a thin walled shell revolted around it's center.
We tried it by using a theorem for thin walled conical shells, but this is not only a very difficult theorem, it also assumes the upper and lower horizontal part to be indeformable; something our feeling says to not be neglect-able.
We assume to be able to find a formula for the vertical movement of the middle as a function of the applied (under) pressure. Does anybody have any suggestions? Can we maybe use a different theorem since our angle "a" is very large?
Schematically represented is the intersection in the following figure:
This is not a difficult exercise if this was just a beam construction. This is however a difficult exercise if it is a thin walled shell revolted around it's center.
We tried it by using a theorem for thin walled conical shells, but this is not only a very difficult theorem, it also assumes the upper and lower horizontal part to be indeformable; something our feeling says to not be neglect-able.
We assume to be able to find a formula for the vertical movement of the middle as a function of the applied (under) pressure. Does anybody have any suggestions? Can we maybe use a different theorem since our angle "a" is very large?