SUMMARY
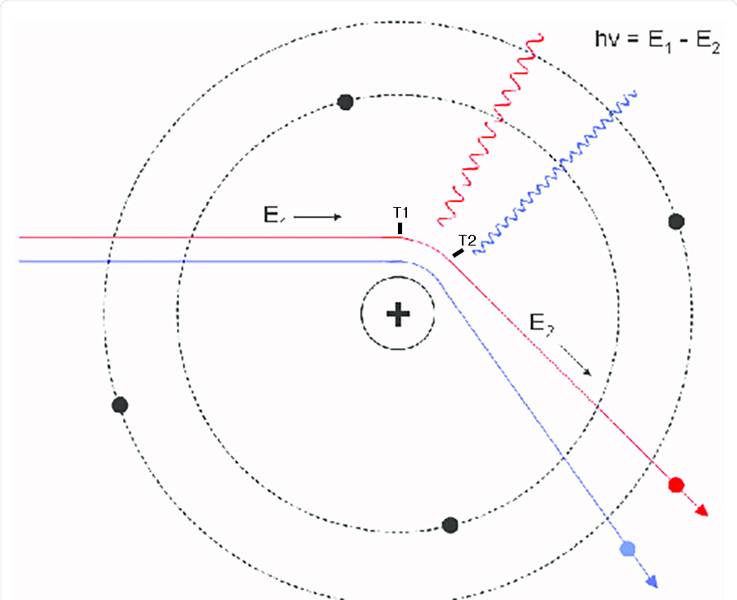
The discussion centers on the implications of electron scattering off a nucleus and the relationship between bremsstrahlung radiation and the electron's momentum change. Participants assert that the infinite range of electromagnetic (EM) forces means that an electron is always accelerating, making it impossible to define a specific time interval for acceleration based on photon frequency. The conversation highlights selection rules for orbital transitions, emphasizing that transitions from a 100s orbital can only occur to certain p orbitals, and clarifies that both photon emission and electron momentum changes do not have well-defined durations. Ultimately, the discussion concludes that classical interpretations of these processes lead to confusion and do not accurately reflect quantum behavior.
PREREQUISITES
- Understanding of bremsstrahlung radiation and its implications in quantum mechanics.
- Familiarity with selection rules for orbital transitions in quantum physics.
- Knowledge of classical versus quantum descriptions of particle interactions.
- Basic principles of electron scattering and momentum vector changes.
NEXT STEPS
- Study the principles of quantum mechanics related to bremsstrahlung radiation.
- Research selection rules for orbital transitions in atomic physics.
- Explore classical and quantum descriptions of electron scattering events.
- Investigate the implications of photon absorption and emission in quantum electrodynamics.
USEFUL FOR
Physicists, quantum mechanics students, and researchers interested in the behavior of electrons in atomic interactions and the nuances of bremsstrahlung radiation.