SUMMARY
This discussion centers on the application of Gauss's law in understanding electric fields within a capacitor. Participants emphasize the importance of clearly defining variables such as the Gauss surface and the distance between capacitor plates. The conversation highlights that if voltage exists across the plates, the electric field cannot be zero, contradicting initial assumptions. The need for clarity in problem formulation and symbol explanation is also stressed, indicating that misinterpretations can lead to confusion in physics problems.
PREREQUISITES
- Understanding of Gauss's law in electromagnetism
- Familiarity with electric fields and potential difference in capacitors
- Knowledge of basic calculus for evaluating integrals
- Ability to interpret and manipulate physics equations
NEXT STEPS
- Review the derivation and application of Gauss's law in different geometries
- Study the relationship between electric field (E), voltage (V), and distance (d) in capacitors
- Explore examples of electric field calculations in cylindrical geometries
- Investigate common pitfalls in physics problem formulation and how to avoid them
USEFUL FOR
Students of physics, educators teaching electromagnetism, and anyone seeking to deepen their understanding of electric fields in capacitors.
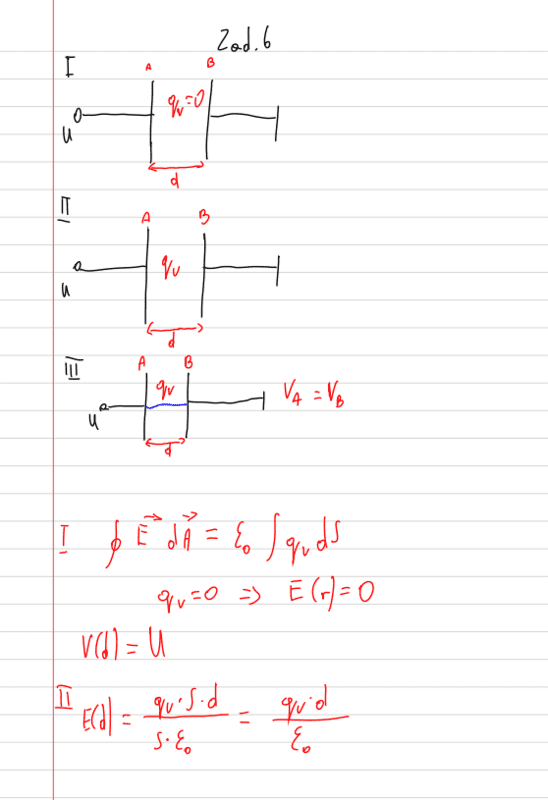
 , but I find 'space charge inside a capacitor' hard to understand. What do you think is meant?
, but I find 'space charge inside a capacitor' hard to understand. What do you think is meant?