- #1
Solarmew
- 37
- 1
Given a join of P3 and C4, "Adjust the picture if necessary so that at most two edges cross in any point (not representing a vertex). Then erect an overpass at every point where two edges of G cross. The genus of G, is the minimum number of overpasses that must be added to the plane so that G can be embedded in the resulting surface."
The objective is to prove that the graph of the join has genus=1, so it can be embedded on a torus. But I can't figure out how to rearrange the vertices in such a way :( I'm assuming there supposed to be only one point of intersection, but the best I can do is three...
Here P3 is 4-6-1, and C4 is 3-7-2-5, but I don't think that's even relevant.
Any help is appreciated.
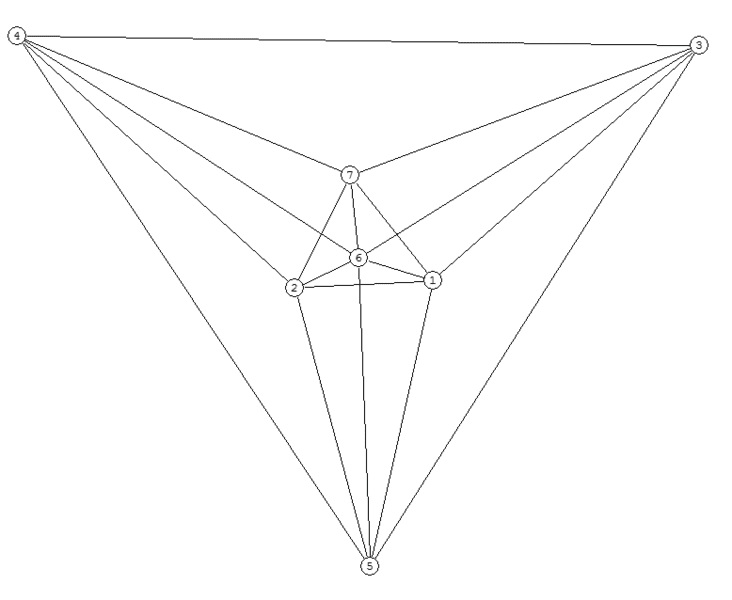
The objective is to prove that the graph of the join has genus=1, so it can be embedded on a torus. But I can't figure out how to rearrange the vertices in such a way :( I'm assuming there supposed to be only one point of intersection, but the best I can do is three...
Here P3 is 4-6-1, and C4 is 3-7-2-5, but I don't think that's even relevant.
Any help is appreciated.