- #1
nickatkins
- 2
- 0
Hi everyone,
I work as a mechanical engineer in Ws Atkins in the analysis and asessment of offshore structures. We are producing a MatchCad spreadsheet at the moment to do what we call a stiffened joint check.
I am posting here to try and get some advice on how to approach and/or solve my problem. I have a solid background in maths and have made some headway.
I will try to give some background to the problem in case anyone is interested :)
background:
A joint is simply the point where two structural members meet, for example a pipe joining onto another pipe.
If you can imagine inside the pipes we sometimes have what are called ring stiffeners, these are internal rings with a web and flange that stiffen the joint to reesist bending moments and shear forces.
Now imagine a smaller pipe joining a larger pipe, the main pipe is called the chord and the smaller joining pipe the brace. The chord is the one that contains stiffeners and can contain several of them. A stiffener only has an effect if it lies within the footprint of the joining brace as it resists incoming forces from the brace by using up its shear capacity. The flange like shape also helps to resist minor axis bending and compression/squashing of the pipe as it increases what's called the 2nd moment of area. In a cross section these internal stiffeners look like a T shape on the inside wall of a pipe. Internal stiffeners are used in a variety of structures not just joints and are similar to adding a web plate to a beam.
Now the problem:
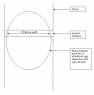
I need to calculate the effective width of the stifferners within the footprint:
see attached image.
Imagaine two circular pipes one of diameter D and one d where D>d.
The smaller pipe intersects the larger one much like in the problem of two intersecting cylinders. In this case however the pipes can intersect at angle theta wherby θ ranges from 0-90 degrees.
Now if you imagine the area of contact of the two pipes eg. If you take a single pipe and take an angled cut you end up with an oval shape yes? we can solve the width of this oval at any point by using the equation of an elipse.
In my case however you do not get an oval shape because the surface is curved in 3 dimensions its like an oval projected onto a cylinder. The shape you actually get is more like an egg shape see my attached picture.
I need to solve the equation of this shape to give x for a given y and also for any given angle. I.e work out the projected width (as if you measured the 2d image) of the shape at any y position and also accounting for the fact that the egg shape is going to vary with the angle theta.
I know its a long shot posting here so I'm looking for advice as to where I should be looking or possible methods I can try to use.
I have found some useful information Ovals and Egg Curves it appears as though i need to add a factor into my elipse equation and this factor will vary with theta.
another approach i thought of was trying to work out the arc lengths at different points along the main pipe but I am not sure how to approach this.
If anyone has any feedback or knows of anyone that can help I would really appreciate your efforts!
Kind Regards
Nick
I work as a mechanical engineer in Ws Atkins in the analysis and asessment of offshore structures. We are producing a MatchCad spreadsheet at the moment to do what we call a stiffened joint check.
I am posting here to try and get some advice on how to approach and/or solve my problem. I have a solid background in maths and have made some headway.
I will try to give some background to the problem in case anyone is interested :)
background:
A joint is simply the point where two structural members meet, for example a pipe joining onto another pipe.
If you can imagine inside the pipes we sometimes have what are called ring stiffeners, these are internal rings with a web and flange that stiffen the joint to reesist bending moments and shear forces.
Now imagine a smaller pipe joining a larger pipe, the main pipe is called the chord and the smaller joining pipe the brace. The chord is the one that contains stiffeners and can contain several of them. A stiffener only has an effect if it lies within the footprint of the joining brace as it resists incoming forces from the brace by using up its shear capacity. The flange like shape also helps to resist minor axis bending and compression/squashing of the pipe as it increases what's called the 2nd moment of area. In a cross section these internal stiffeners look like a T shape on the inside wall of a pipe. Internal stiffeners are used in a variety of structures not just joints and are similar to adding a web plate to a beam.
Now the problem:
I need to calculate the effective width of the stifferners within the footprint:
see attached image.
Imagaine two circular pipes one of diameter D and one d where D>d.
The smaller pipe intersects the larger one much like in the problem of two intersecting cylinders. In this case however the pipes can intersect at angle theta wherby θ ranges from 0-90 degrees.
Now if you imagine the area of contact of the two pipes eg. If you take a single pipe and take an angled cut you end up with an oval shape yes? we can solve the width of this oval at any point by using the equation of an elipse.
In my case however you do not get an oval shape because the surface is curved in 3 dimensions its like an oval projected onto a cylinder. The shape you actually get is more like an egg shape see my attached picture.
I need to solve the equation of this shape to give x for a given y and also for any given angle. I.e work out the projected width (as if you measured the 2d image) of the shape at any y position and also accounting for the fact that the egg shape is going to vary with the angle theta.
I know its a long shot posting here so I'm looking for advice as to where I should be looking or possible methods I can try to use.
I have found some useful information Ovals and Egg Curves it appears as though i need to add a factor into my elipse equation and this factor will vary with theta.
another approach i thought of was trying to work out the arc lengths at different points along the main pipe but I am not sure how to approach this.
If anyone has any feedback or knows of anyone that can help I would really appreciate your efforts!
Kind Regards
Nick