Energy Conservation/Potential Energy - block on a hill

[lakersoftball]

Homework Statement

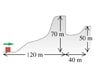
A 2.8kg block slides over a smooth icy hill. The top of the hill is horizontal and 70m higher than its base. The 70m plateau is 80m from the base of the hill. What is the minimum speed the block must have so that it will not fall into the pit on the far side of the hill?

(Picture attached)

Homework Equations

PE = mgh
K = .5mv^2

The Attempt at a Solution

mgh = .5mv^2
(2.8)(9.8)(70) = .5(2.8)v^2
3841.6 = v^2

v = 37 m /s


This answer is not right, I am not very strong in physics and frankly don't even know if I am using the correct formulas. Anything helps, thanks :]

 

[Doc Al]

mgh = .5mv^2
(2.8)(9.8)(70) = .5(2.8)v^2
3841.6 = v^2

v = 37 m /s

What you solved for is the speed the block needs at the bottom to just barely make it to the top. But what they want is the minimum speed to send it sailing over the top and completely miss the hole on the other side. So treat the block as a projectile as it leaves the highest point: First figure out what speed it needs at the top to make it across the hole without falling in. Then you can worry about the speed it needs to start with at the bottom.