Starting height of marble rolling around a loop the loop

[Jamie_Pi]

Homework Statement

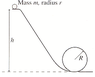
The marble rolls down a track and around a loop-the-loop of radius R. The marble has mass m and radius r. What minimum height h must the track have for the marble to make it around the loop-the-loop without falling off? (Use any variable or symbol stated above along with the following as necessary: g.)

Homework Equations

KE=1/2mv^2+1/2I*w^2
KE+PE+W=KE+PE+∆Eth
mv^2/r=centripetal force
w=v/r

The Attempt at a Solution

I started by imagining the marble was already at the bottom of the hill. What does the marble need to get all the way around the loop the loop? I set the kinetic energy of the ball at the bottom of the hill equal to the kinetic energy of the ball at the top of the loop plus the potential energy at the top of the loop:
KEi=KEf+PEf
Where KEi is the kinetic energy of the marble at the bottom of the hill and KEf is the kinetic energy at the top of the loop and PEf is the potential energy at the top of the loop. I imagined I could use this to solve for the potential energy at the top of the hill, since that should be equal to the kinetic energy at the bottom of the hill.
To solve for PEf, I used PE=mg*h, in this context, PEf=mg*2R (the height of the loop).

To solve for kinetic energy, I found the velocity required to loop the loop:
mv^2/R=mg (The centripetal force needs to exactly equal the force of gravity)
Therefore, v=sqrt(g*R).
I plugged this into KE=1/2mv^2+1/2Iw^2 (using the moment of inertia for a sphere) to get
KEf=1/2m*v^2+1/2*2/5mr^2*v^2/r^2 which becomes
KEf=1/2mgR+1/5mgR (plugging my value for v and simplifying)
So, I figure I'm done here. I put these back into my conservation of energy equation:
KEi=1/2mgR+1/5mgR+mg2R
And I think, "Well, I can assume that the marble fell from height h to get this kinetic energy, so all of the initial starting potential energy must have been converted into kinetic energy. Therefore, the starting potential energy must be equal to this kinetic energy."
And I write down:
PEi=KEf (what was once KEi is now KEf) which becomes
mgh=1/2mgR+1/5mgR+2mgR

h=R(1/2+1/5+2)

Which is wrong. I'm really appreciative that any of you read this whole thing, if you could point out any mistakes or wrong assumptions that I made, I'd be super thankful!

 

[haruspex]

PEf=mg*2R

Not quite. This is not a point particle.

 

[RedDelicious]

You almost have it, but you need to take into account the radius of the marble when finding potential energy.

Edit: I missed that this was already posted, didn't mean to bump with basically the same exact thing.

 

[Jamie_Pi]

Not quite. This is not a point particle.

Ok, so instead of saying
mgh=R(1/2+1/5+2) I'll say
mg(h+r)=R(1/2+1/5+2) getting
h=R(1/2+1/5+2)-r

But that isn't right either, so I must be missing something. I can't find any other definition of gravitational potential energy online other than U=mgh.

 

[haruspex]

mg(h+r)

Still not quite there. Compare the initial position with the top-of-loop position.
You also need to consider how the centripetal acceleration is affected.

 

[Jamie_Pi]

Still not quite there. Compare the initial position with the top-of-loop position.
You also need to consider how the centripetal acceleration is affected.

Ahhh, I think I understand:
KEi=1/2mg(R-r)+1/5mg(R-r)+2mg(R-r)
and
PE=mg(h+r)
meaning that
h=(R-r)(1/5+1/2+2)-r

Is that right?

 

[haruspex]

Still not quite. You have not corrected this:

PE=mg(h+r)

It might help to consider the extreme case, r=R.

 

[Jamie_Pi]

It might help to consider the extreme case, r=R.

Is it
mg(h-r)?
I'm not really sure what to do other than that.

 

[haruspex]

Is it
mg(h-r)?
I'm not really sure what to do other than that.

Try drawing a diagram with h=2R. Compare the initial and final positions of the marble. How much has it dropped?

 

[Jamie_Pi]

Try drawing a diagram with h=2R. Compare the initial and final positions of the marble. How much has it dropped?

Ok, I drew this: (sorry, poor quality)

And from the top of the hill, it seems that the marble falls as far as h is, which makes sense.
So is the potential energy at the top of the hill equal to mgh, but at the top of the loop equal to 2(R-r)? That would make the equation:
h=(R-r)(1/2+1/5+2)

 

[haruspex]

Ok, I drew this: (sorry, poor quality)
View attachment 214299
And from the top of the hill, it seems that the marble falls as far as h is, which makes sense.
So is the potential energy at the top of the hill equal to mgh, but at the top of the loop equal to 2(R-r)? That would make the equation:
h=(R-r)(1/2+1/5+2)

Yes. It's the 2r drop, rather than r, that you were missing.

 

[Jamie_Pi]

Yes. It's the 2r drop, rather than r, that you were missing.

Ok, I see. Thanks! You've been a big help.

 

[haruspex]

Ok, I see. Thanks! You've been a big help.

One interesting point about the answer... even if we let r tend to zero, the 1/5 term is still there. It is a common error to assume that if r<<R then the rotational energy can be ignored.