JonAce73
- 6
- 0
- TL;DR
- What is the relative values of the transition matrix as defined in [2] during the polarization detection and before the entanglement swapping described in [1]?
I would highly appreciate it if you can answer my questions below on entanglement swapping described in [1] in the context of Indivisible Stochastic Processes explained in [2]. The symbols below should be interpreted as in Latex.
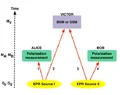
Suppose in figure 2 (attached) of [1], the two pairs of entangled photons (1,2) and (3,4) constitute the subject system $S$ while the polarization measuring devices named Alice and Bob, and the analyzer, which randomly performs the Bell-state measurement (BSM) or not, constitute the environment $E$ to which $S$ interacts. Suppose the photons are emitted at time zero. Then at time $t'$ photons 1 and 4 interact with Alice and Bob, respectively. Let the transition matrix, as defined in [2], from time zero to $t'$ be $\Gamma^S(t' \leftarrow 0)$ where at $t'$ BSM is not applied to photons 2 and 3 yet at the analyzer. Now, at time $t$ photons 2 and 3 undergo BSM thereby they are projected into one of the entangled Bell-states and the remaining photons 1 and 4 are projected into an entangled Bell-state as well. Let the transition matrix from time $t'$ to $t$ of $S$ be $\Gamma^S(t \leftarrow t')$. Thus, the transition matrix from time zero to $t$ is $\Gamma^S(t \leftarrow 0) = \Gamma^S(t \leftarrow t') \Gamma^S(t' \leftarrow 0)$, i.e., similar to Eq. 56 of [2].
Let $C'$ be the configuration having photons 1 and 2 entangled, and photons 3 and 4 entangled; and $C^t$ be the configuration having photons 1 and 4 in an entangled Bell-state, and photons 2 and 3 as well. Should $\Gamma^S(t' \leftarrow 0)$ (i.e., the transition matrix from time zero to the interaction time $t'$ at Alice and Bob) for configuration $C'$ be lesser than for configuration $C^t$ when in the future time $t$ BSM is applied (or not) on photons 2 and 3 at the analyzer?
My problem is, the relative values of the respective transition matrices for the two configurations cannot be determined prior to the random BSM application (or not) on photons 2 and 3. Perhaps, the matrices cannot be known until the interaction at the analyzer; or I misunderstood [2].
Thanks for entertaining my questions.
[1] D. Glick, “Timelike entanglement for delayed-choice entanglement swapping,” Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, vol. 68, pp. 16–22, 2019.
[2] J. A. Barandes, “The stochastic-quantum correspondence,” arXiv preprint arXiv:2302.10778, 2023.
Suppose in figure 2 (attached) of [1], the two pairs of entangled photons (1,2) and (3,4) constitute the subject system $S$ while the polarization measuring devices named Alice and Bob, and the analyzer, which randomly performs the Bell-state measurement (BSM) or not, constitute the environment $E$ to which $S$ interacts. Suppose the photons are emitted at time zero. Then at time $t'$ photons 1 and 4 interact with Alice and Bob, respectively. Let the transition matrix, as defined in [2], from time zero to $t'$ be $\Gamma^S(t' \leftarrow 0)$ where at $t'$ BSM is not applied to photons 2 and 3 yet at the analyzer. Now, at time $t$ photons 2 and 3 undergo BSM thereby they are projected into one of the entangled Bell-states and the remaining photons 1 and 4 are projected into an entangled Bell-state as well. Let the transition matrix from time $t'$ to $t$ of $S$ be $\Gamma^S(t \leftarrow t')$. Thus, the transition matrix from time zero to $t$ is $\Gamma^S(t \leftarrow 0) = \Gamma^S(t \leftarrow t') \Gamma^S(t' \leftarrow 0)$, i.e., similar to Eq. 56 of [2].
Let $C'$ be the configuration having photons 1 and 2 entangled, and photons 3 and 4 entangled; and $C^t$ be the configuration having photons 1 and 4 in an entangled Bell-state, and photons 2 and 3 as well. Should $\Gamma^S(t' \leftarrow 0)$ (i.e., the transition matrix from time zero to the interaction time $t'$ at Alice and Bob) for configuration $C'$ be lesser than for configuration $C^t$ when in the future time $t$ BSM is applied (or not) on photons 2 and 3 at the analyzer?
My problem is, the relative values of the respective transition matrices for the two configurations cannot be determined prior to the random BSM application (or not) on photons 2 and 3. Perhaps, the matrices cannot be known until the interaction at the analyzer; or I misunderstood [2].
Thanks for entertaining my questions.
[1] D. Glick, “Timelike entanglement for delayed-choice entanglement swapping,” Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, vol. 68, pp. 16–22, 2019.
[2] J. A. Barandes, “The stochastic-quantum correspondence,” arXiv preprint arXiv:2302.10778, 2023.