Epsilon-Delta definition property.

[Alpharup]

he

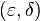definition of the limit of a function is as follows:[5]

Let

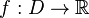be a function defined on a subset [PLAIN]https://upload.wikimedia.org/math/a/1/b/a1b67abab803e714098f3e69a33900da.png, let

be a limit point of [PLAIN]https://upload.wikimedia.org/math/f/6/2/f623e75af30e62bbd73d6df5b50bb7b5.png, and let

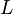be a real number. Then

the function

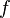has a limit

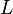at

is defined to mean

for all [PLAIN]https://upload.wikimedia.org/math/b/0/f/b0f19c5714fe9f9891ed26ff783cf639.png, there exists a https://upload.wikimedia.org/math/1/c/b/1cb24dafc8035d2c720256620066ae73.png such that for all

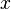in

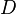that satisfy [PLAIN]https://upload.wikimedia.org/math/6/e/e/6ee6dc9ee03f04da6ff784b6eca416e5.png, the inequality https://upload.wikimedia.org/math/2/c/4/2c412a6f49514db4dbd890537413bcc6.png holds.
.

Taken from https://en.wikipedia.org/wiki/(ε,_δ)-definition_of_limit

The problem what Iam facing is the statement ," for all

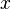in

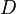that satisfy [PLAIN]https://upload.wikimedia.org/math/6/e/e/6ee6dc9ee03f04da6ff784b6eca416e5.png". Though I have understood this statement, this hinders my proving this property of limit

lim f(c+h)=L =lim f(x).
h->0 x->c

I am trying to prove the LHS from the RHS.

We know,

"the function f has a limit L at

is defined to mean
for every ε>0,there exists a δ>0, sucht that, for all x in D satisfying, o<|x-a|<δ, implies |f(x)-L|<ε.The LHS can be proven from the trivial fact taking
x-c=h.
A question arises to me. How do we know the existence of such an h? Also, for what all h does this inequality o<|h|<δ implies |f(c+h)-L|<ε hold?

 

[HallsofIvy]

You are taking h= x- c so "h goes to 0" is the same as "x goes to c" or $|h|< \delta$ is the same as $|c+ h|< \delta$. In more detail, if $|h|< \delta$ then $-\delta< h< \delta$ so that $-\delta< x- c< \delta$ and vice-versa.

 

[Alpharup]

$|h|< \delta$ is the same as $|c+ h|< \delta$.

How is this possible?

 

[Ssnow]

The fact is that you change variable but the limit remains the same, by assumptions you have $\lim_{x\rightarrow c} f(x)=L$ if you change variable, you can set as example $x=c+h$, so when $x\rightarrow c$ you have $h\rightarrow 0$ and the limit become:
$\lim_{h\rightarrow 0} f(c+h)=L$ ... , such $h$ exists (because the difference $x-c$ always exists and you call it with the letter $h$), therefore $0<|h|<\delta$ and from $\left|f(x)-L\right|<\varepsilon$ you have $\left|f(c+h)-L\right|<\varepsilon$ ...

It is only a way to rewrite the limit from the variable $x$ to the new variable $h$, in fact $c$ is a number always fixed and I suppose finite ...

 

[Alpharup]

@Ssnow
You are right. Such an h exists like h=x-c.
But what is the condition 'h' should satisfy? How do convert the statement "for all x satisfying 0<|x-c|<δ" to "for all h satisfying 0<|h|<δ"
Other statements in the epsilon-delta definition make sense except this statement. Can we convert from "all x" to "all h"?

 

[Ssnow]

Yes, now you point is $0$ so for all $h$ satisfying $0<|h-0|<\delta$ ...

 

[HallsofIvy]

How is this possible?

Oops! I meant to write $|h|< \delta$ is the same as $|x- c|< \delta$.

 

[Alpharup]

Yes, logically it is right. But, i need conversion of statement. I thought of this proof. Please say whether it is right.
All the numbers are real in this discussion.
Because of exsistance property of h for any real numbers x and c, we can write:
For all real x and all real c, there exists an unique(one and only one) h such that h=x-c.
Let us take an x which satisfies 0<|x-c|< δ. Let it be x1. By definition, we have "for all x satisfying the property P". So, we can take an arbitray x =x1 satisying that property.
For this x1 and c, we have an unique h=h1 such that h1=x1-c.
By induction,we can prove that for a xn(satisfying P) and c, we have an unique hn such that hn=xn-c.
x can be x1,x2...xn(which satisfying P)
h can be h1,h2,...hn(which are unique for a given x).
So, by induction we can say, "for every x, we can find, every h."

 

[Ssnow]

yes, but I think the existence it is clear because $x,c$ exists so also the difference exists in $\mathbb{R}$. To prove the unicity of $h$ you can procede by contradiction argument. Assume that there are two $h_{1},h_{2}$ such that $h_{1}=x-c$ and $h_{2}=x-c$, then it is clear that $h_{1}=h_{2}$, so is unique ...

 

[Alpharup]

Good proof of uniqueness theorem...