Lancelot1
- 26
- 0
Dear All,
I am trying to solve the attached two questions.
In both I need to determine if the relation is an equivalence relation, to prove it if so, and to find the equivalence classes.
In both cases it is an equivalence relation, and I managed to prove both relations are reflexive. Now I am with symmetry and transitivity. In the first case, it is obviously symmetric, but how do I prove it ? Same for the second relation, I find it hard to prove and also to prove transitivity.
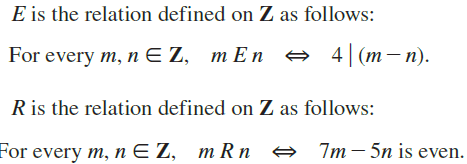
For reflexivity, m-m = 0 which is dividable by 4. Also 7m-5m=2m, which is dividable by 2 and therefore even.
Thank you !
I am trying to solve the attached two questions.
In both I need to determine if the relation is an equivalence relation, to prove it if so, and to find the equivalence classes.
In both cases it is an equivalence relation, and I managed to prove both relations are reflexive. Now I am with symmetry and transitivity. In the first case, it is obviously symmetric, but how do I prove it ? Same for the second relation, I find it hard to prove and also to prove transitivity.
For reflexivity, m-m = 0 which is dividable by 4. Also 7m-5m=2m, which is dividable by 2 and therefore even.
Thank you !