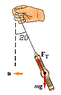SUMMARY
The discussion focuses on estimating the takeoff speed of an aircraft using physics principles. Francesca observes that her watch hangs at a 20° angle during takeoff, prompting calculations involving gravitational force and the aircraft's acceleration. The key formula derived is a = g * tan(20°), where g is the acceleration due to gravity (9.8 m/s²). Participants conclude that the final velocity can be calculated using the formula Vf = Vi + at, leading to a takeoff speed of approximately 390 m/s after 14.5 seconds of acceleration.
PREREQUISITES
- Understanding of basic physics concepts, including forces and acceleration.
- Familiarity with vector representation of forces.
- Knowledge of trigonometric functions, specifically tangent.
- Ability to apply kinematic equations in physics.
NEXT STEPS
- Study the application of Newton's second law in real-world scenarios.
- Learn more about kinematic equations and their applications in physics.
- Explore the relationship between angles and forces in vector analysis.
- Investigate the effects of different angles of climb on aircraft performance.
USEFUL FOR
Physics students, aerospace engineers, and anyone interested in the dynamics of aircraft takeoff and acceleration calculations.