guyvsdcsniper
- 264
- 37
- Homework Statement
- Find the potential V (x,y) at all points across the section of this pipe.
- Relevant Equations
- dv/dx=0
I have attached an image of the pipe in the attachmnts. The pipe is parallel to z-axis form (-∞,∞) and sides of length a.
So my boundary conditions for this problem are as follows
1.) V=0 at y=0
2.)V=0 at y=a
4.)∂v/∂x=0 @ x=0
3.)V0 @ x=a
I am a little confused on the fourth boundary condition only because my answer doesn't seem to match up with what I have found on the internet.
When solving B.C 4 and simplify i get, V0=Csin(nπy/a)(cosh(nπ)/2)
The answer I found gives V0=2Csin(nπy/a)(cosh(nπ))
Im not sure how they are getting the equation to be a multiple of 2 when the identity of (ex+e-x)=cosh(x)/2
The solution I found is the image that looks scanned. My work is the image that is in blue and black ink.
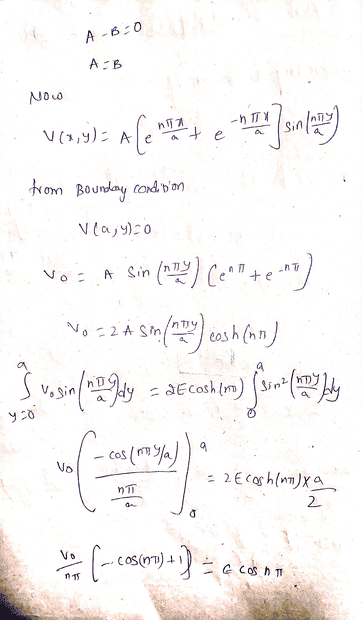
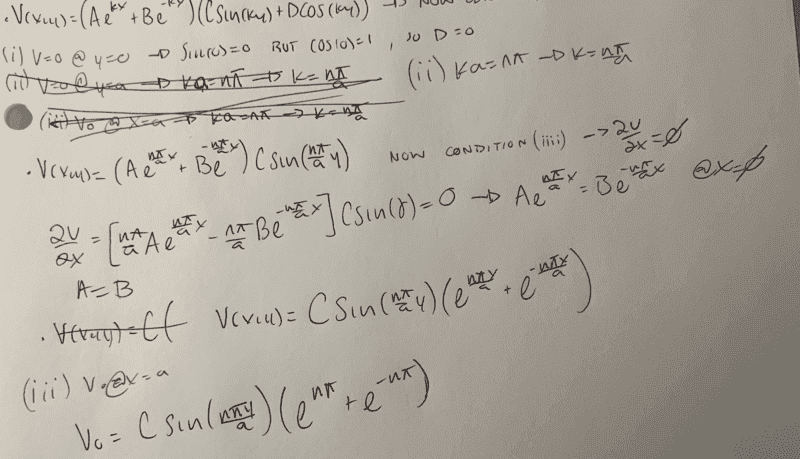

So my boundary conditions for this problem are as follows
1.) V=0 at y=0
2.)V=0 at y=a
4.)∂v/∂x=0 @ x=0
3.)V0 @ x=a
I am a little confused on the fourth boundary condition only because my answer doesn't seem to match up with what I have found on the internet.
When solving B.C 4 and simplify i get, V0=Csin(nπy/a)(cosh(nπ)/2)
The answer I found gives V0=2Csin(nπy/a)(cosh(nπ))
Im not sure how they are getting the equation to be a multiple of 2 when the identity of (ex+e-x)=cosh(x)/2
The solution I found is the image that looks scanned. My work is the image that is in blue and black ink.