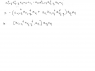Fermionic Operator Equation Derivation Troubleshooting

[aaaa202]

Attached is a derivation of the equation of motion for the fundamental fermionic anihillation opeator but I am having a bit of trouble with the notation.
Does the notation V_v2-v and the other V_ simply mean that all terms in the sum of q have canceled except for when q=v₂-v or v-v₁?
And second of all: Isn't the middle equation wrong for v=v₁? Because then to move the a_v1 you only have to anticomutte it once which yields a minus sign which is not canceled out by further anticommuting it.

 

[strangerep]

Does the notation V_v2-v and the other V_ simply mean that all terms in the sum of q have canceled except for when q=v₂-v or v-v₁?

No, it just means that you've got a triple sum. Write it out explicitly for the case when there's only a small number of fermion modes (i.e., when all summations are over 1,2 only).

And second of all: Isn't the middle equation wrong for v=v₁? Because then to move the a_v1 you only have to anticomutte it once which yields a minus sign which is not canceled out by further anticommuting it.

Exactly which part of the middle equation do you think is wrong? Show your work here.

 

[aaaa202]

What do you mean triple sum? there is no q in the sum anymore, so haven't all terms disappeared except for the two terms I indicated?
For v1=v the term in the sum yields the attached which cannot be written as the commutator suggested.

 

[ChrisVer]

what do you get by calculating the commutator? of course you will get a delta Kroenecker...

 

[strangerep]

What do you mean triple sum? there is no q in the sum anymore, so haven't all terms disappeared except for the two terms I indicated?

I have no idea what you mean by this. I see a triple sum everywhere except the last line. Please write it out properly, in latex, so I can see exactly which expressions you refer to. I'm not interested in guessing what you mean, and I also have a bit of trouble with your handwriting. (If you won't make an effort to learn and use basic latex on this forum, and express your questions more explicitly, then why should others make an effort to help you? Instructions for getting started with latex can be found by on the main PF page by following SiteInfo->FAQ... )

For v1=v the term in the sum yields the attached which cannot be written as the commutator suggested.

By focusing just on $\nu_1 = \nu$ you're not seeing the full picture. If you want more help, then do the following:

1) Write out the basic anticommutators that $a$'s and $a^\dagger$'s satisfy.

2) Write your Hamiltonian as $H = T + V$ (where $T$ is the free part, and $V$ is the current-current interaction part).
Then work out $[T,a_\lambda]$ separately, showing all steps.

3) Then work out $[V, a_\lambda]$ separately, showing all steps.

 

[aaaa202]

Well it's just that I can't see how focusing on the big picture would mend the problem. I have tried to look at v=v2 to see if that should somehow cancel out the bad minus but no. And since all other v's commute they can't fix it either. I have been staring for half an hour at that equation. I won't ask you to do it for me - but can you say with words what fixes the minus that I pointed out would make make the equality wrong.

 

[strangerep]

Well it's just that I can't see how focusing on the big picture would mend the problem.

Sometimes, you've just got to trust the person who is trying to help you, even if you can't "see" how it would help.

You would have been far better off if you'd spent that half-hour doing what I suggested, instead of resisting me.
(This is a really easy problem, btw. I should have insisted this thread be moved to the homework forums.)

 

[aaaa202]

Okay I finally found out. The fermionic operators anticommute even when the subscripts are the same. Why didn't you just tell me this? Going down your way, which I actually did, I wouldn't have figured out that aa=-aa...

 

[strangerep]

Okay I finally found out. The fermionic operators anticommute even when the subscripts are the same. Why didn't you just tell me this?

Because I'm not a mind reader.

Going down your way, which I actually did, I wouldn't have figured out that aa=-aa...

Yes, it would have. I knew you had a stubborn mental block somewhere, but I didn't know exactly where. My suggestions were designed to diagnose your problem, if you were willing to devote some effort.

You must understand that I won't put much effort into helping you while you refuse to put effort into learning and using latex on this forum, and showing more of your work.