- #1
gtavictor
- 7
- 0
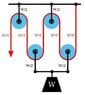
Hello people, this is my first post here in PF and I have a problem with the modeling of a pulley system considering the friction between wire and pulley. I have a similar system as show in the image below and I have a friction factor of 0.25 between wire and pulley, my question is, how can I model an equation to find the force at the open end of the wire to move the weight?
http://img52.imageshack.us/img52/9240/534pxpulley3asvg.jpg
thanks in advance!
EDIT: Please at least do not consider the value of the friction, I just want to make the modeling of the force necessary to move the weight due to friction losses!
http://img52.imageshack.us/img52/9240/534pxpulley3asvg.jpg
thanks in advance!
EDIT: Please at least do not consider the value of the friction, I just want to make the modeling of the force necessary to move the weight due to friction losses!
Last edited by a moderator: