Find accelerations- Angular and linear

[cbarker1]

Dear Every Body,

I need some help. First question: Is the tension of the string is the same or different?
A pulley of moment of inertia 2.7 kg [FONT=&quot]· m² is mounted on a wall as shown in the following figure. Light strings are wrapped around two circumferences of the pulley and weights are attached. Assume the following data: r₁ = 47 cm,
r₂ = 20 cm,
m₁ = 1.0 kg,
and m₂ = 1.9 kg.

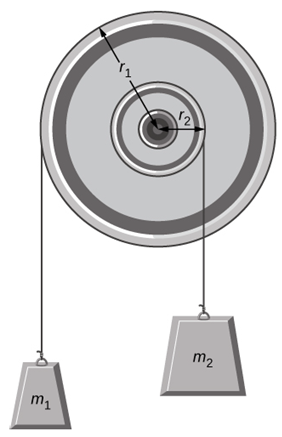(a)
What is the angular acceleration in rad/$s^2$ of the pulley?


(b)
What is the linear acceleration (in m/s²) of the weights?
a₁

a₂

 

[I like Serena]

Hi Cbarker1,

Which formulas do you have that:
- relate torque to angular acceleration?
- relate torque to force?

Can we apply them?

 

[cbarker1]

Hi Cbarker1,

Which formulas do you have that:
- relate torque to angular acceleration?
- relate torque to force?

Can we apply them?

$\Sigma \tau=I\alpha$
$\tau=Fr$
$\Sigma F=ma$
For the first hanging mass:
$m_1g-T=m_1a_1$
$T=m_1g-m_1a_1$
For the second hanging mass:
$T=m_2a_2+m_2g$

 

[I like Serena]

$\Sigma \tau=I\alpha$
$\tau=Fr$
$\Sigma F=ma$
For the first hanging mass:
$m_1g-T=m_1a_1$
$T=m_1g-m_1a_1$
For the second hanging mass:
$T=m_2a_2+m_2g$

Good!
We also need that the speed of both masses match the speed that the wheel turns (where the masses are attached).
Can we also catch those in formulas?

 

[cbarker1]

Do the mass have same tension?

 

[I like Serena]

Do the mass have same tension?

If the system were in equilibrium, the corresponding torques would have to cancel.
Since they are at different distances, that means that in equilibrium the tensions have to be different.
So we can't assume that the tensions are the same, and we have to keep them like $T_1$ and $T_2$ instead of just $T$.

 

[cbarker1]

If the system were in equilibrium, the corresponding torques would have to cancel.
Since they are at different distances, that means that in equilibrium the tensions have to be different.
So we can't assume that the tensions are the same, and we have to keep them like $T_1$ and $T_2$ instead of just $T$.

$$T_2=1.9a_2+1.9g$$
$$T_1=g-a_1$$
$$T_1r_1+T_2r_2=I\alpha $$

 

[I like Serena]

$$T_2=1.9a_2+1.9g$$
$$T_1=g-a_1$$
$$T_1r_1+T_2r_2=I\alpha $$

Let's be careful with our signs.
The tensions that act on the masses both point upward yes?
Ideally we pick a direction up or down that we call positive and then stick to it.
How about picking 'up' to be 'positive' (it seems you already did)?

Which directions did you pick for $a_1$ and $a_2$?
Since we don't know yet if they are up or down, can we pick them both to be in the 'positive' direction?
If we do, there is a sign that we need to correct.

As for the angular acceleration, the torques oppose each other do they not?
That means one of them should have a minus sign.

Can we also include 2 more equations for the speeds of the masses that each must equal the speed of the wheel where the strings attach?

 

[cbarker1]

I think $$a_1$$ should be positive and $$a_2$$ should be negative.

 

[I like Serena]

I think $$a_1$$ should be positive and $$a_2$$ should be negative.

That's also fine.
A drawing would be nice then, since otherwise I have no clue which vector points where.

 

[cbarker1]

here is the picture