Find coordinates of f′, f′′, f′′′ in the basis

[Logan Land]

Consider the polynomial f(x) = x^5 − 5x^4.

(a) Find coordinates of f′, f′′, f′′′ in the basis {1, x, x2, x3, x4, x5}

I no f ' = 5x^4-20x^3
f " = 20x^3-60x^2
and f "' = 60x^2-120x

but from there where to begin?

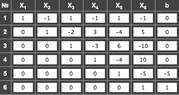
do I make a matrix of like the following?

1 0 0 0 0 0 0
0 1 0 0 0 0 0
0 0 1 0 0 0 0
0 0 0 1 0 0 -20
0 0 0 0 1 0 5
0 0 0 0 0 1 0

cause that is already in reduced form.

Just a little confused on where to start after find f ' , f " , and f '''
unless the coordinate vector is just
(0,0,0,-20,5,0) for f ' ?

 

[Euge]

unless the coordinate vector is just
(0,0,0,-20,5,0) for f ' ?

Yes, that's right. So how would you write the coordinates of $f''$ and $f'''$, knowing that $f''(x) = 20x^3 - 60x^2$ and $f'''(x) = 60x^2 - 120x$?

 

[Logan Land]

Yes, that's right. So how would you write the coordinates of $f''$ and $f'''$, knowing that $f''(x) = 20x^3 - 60x^2$ and $f'''(x) = 60x^2 - 120x$?

f '' = (0,0,-60,20,0,0)?
f ''' = (0,-120,60,0,0,0)?

Hope that's correct

-----------------

If my basis was
{1,(x−1),(x−1)^2,(x−1)^3,(x−1)^4,(x−1)^5}

would I expand the factors and create a matrix with the f, f ' , f '' in the last column and solve to get the coordinates for each f, f ' and f ''?

 

[Euge]

f '' = (0,0,-60,20,0,0)?
f ''' = (0,-120,60,0,0,0)?

Hope that's correct

Yes, that's right.

If my basis was
{1,(x−1),(x−1)^2,(x−1)^3,(x−1)^4,(x−1)^5}

would I expand the factors and create a matrix with the f, f ' , f '' in the last column and solve to get the coordinates for each f, f ' and f ''?

The coefficients of the Taylor series of $f$ at $x = 1$ are $a_n = \frac{f^{(n)}(1)}{n!}$, for all integers $n \ge 0$. Since $f$ is a polynomial of degree 5, $a_n = 0$ for $n > 5$. So the coordinates of $f$ relative to your new basis is $(a_0, a_1, a_2, a_3, a_4, a_5)$. Find the values of these $a_n$. Apply this method to $f'$ and $f''$ to find their coordinates.

 

[Logan Land]

Yes, that's right.
The coefficients of the Taylor series of $f$ at $x = 1$ are $a_n = \frac{f^{(n)}(1)}{n!}$, for all integers $n \ge 0$. Since $f$ is a polynomial of degree 5, $a_n = 0$ for $n > 5$. So the coordinates of $f$ relative to your new basis is $(a_0, a_1, a_2, a_3, a_4, a_5)$. Find the values of these $a_n$. Apply this method to $f'$ and $f''$ to find their coordinates.

So my $a_1 = \frac{1^{(1)}(1)}{1!}$ is the answer to this? Sorry that confused me a little. Our teach never mentioned that.

 

[Euge]

The symbol $f^{(n)}$ means the $n$th derivative of $f$. When $n = 0$, $f^{(n)} = f$.

 

[Logan Land]

The symbol $f^{(n)}$ means the $n$th derivative of $f$. When $n = 0$, $f^{(n)} = f$.

How do I put that into that equation when there's 2 values of x powers, x^5 and x^4 or do I do each separately?
Could I see an example possibility?

Thanks

 

[Euge]

How do I put that into that equation when there's 2 values of x powers, x^5 and x^4 or do I do each separately?
Could I see an example possibility?

Thanks

We have

$$a_0 = f(1) = 1 - 5 = -4$$

$$a_1 = f'(1) = 5 - 20 = -15$$

$$a_2 = \frac{f''(2)}{2} = \frac{20 - 60}{2} = -20$$

Since $f'''(x) = 60x^2 - 120x$, $f'''(1) = 60 - 120 = -60$ and thus

$$a_3 = \frac{f'''(1)}{6} = -10$$

Can you compute $a_4$ and $a_5$?

 

[Logan Land]

We have

$$a_0 = f(1) = 1 - 5 = -4$$

$$a_1 = f'(1) = 5 - 20 = -15$$

$$a_2 = \frac{f''(2)}{2} = \frac{20 - 60}{2} = -20$$

Since $f'''(x) = 60x^2 - 120x$, $f'''(1) = 60 - 120 = -60$ and thus

$$a_3 = \frac{f'''(1)}{6} = -10$$

Can you compute $a_4$ and $a_5$?

Would a4 be 0? Since we have (120x-120)/24 or 0/24 =0?

And

A5= 120/120 or 1?

 

[Euge]

Would a4 be 0? Since we have (120x-120)/24 or 0/24 =0?

And

A5= 120/120 or 1?

Yes, $a_4 = 0$ and $a_5 = 1$. So what are the coordinates of $f$?

 

[Logan Land]

Yes, $a_4 = 0$ and $a_5 = 1$. So what are the coordinates of $f$?

(-4,-15,-20,-10,0,1)??

 

[Euge]

(-4,-15,-20,-10,0,1)??

Excellent! :)

 

[Logan Land]

Excellent! :)

If that's the coordinates for f then how do I get f' and f" coordinates if i used derivatives of f to get f coordinates?

 

[Logan Land]

If that's the coordinates for f then how do I get f' and f" coordinates if i used derivatives of f to get f coordinates?

or do I start with f ' as a0 then go from there to obtain the coordinates for f'?

and for f '' start with f '' as a0 then go from there to obtain the coordinates for f ''?

 

[Euge]

If that's the coordinates for f then how do I get f' and f" coordinates if i used derivatives of f to get f coordinates?

Now you know that

$$f(x) = -4 - 15(x - 1) - 20(x - 1)^2 - 10(x - 1)^3 + (x - 1)^5.$$

Differentiate this equation, using the property $\frac{d}{dx}(x - 1)^n = n(x - 1)^{n-1}$ (which follows from the chain rule):

$$f'(x) = -15 - 40(x - 1) - 30(x - 1)^2 + 5(x - 1)^4.$$

So $(-15, -40, -30, 0, 5, 0)$ make the coordinates for $f'$. Using the same method you can find the coordinates for $f''$.

 

[Logan Land]

Now you know that

$$f(x) = -4 - 15(x - 1) - 20(x - 1)^2 - 10(x - 1)^3 + (x - 1)^5.$$

Differentiate this equation, using the property $\frac{d}{dx}(x - 1)^n = n(x - 1)^{n-1}$ (which follows from the chain rule):

$$f'(x) = -15 - 40(x - 1) - 30(x - 1)^2 + 5(x - 1)^4.$$

So $(-15, -40, -30, 0, 5, 0)$ make the coordinates for $f'$. Using the same method you can find the coordinates for $f''$.

so in this case would f '' be (-40,-60,0,20,0,0)?

 

[Euge]

so in this case would f '' be (-40,-60,0,20,0,0)?

Correct!

 

[Logan Land]

Correct!

Perfect!

I can see that this is a faster method but would it also work if I expanded the factors into polynomials and put them in matrix form in a 6x7 matrix with column 7 the f(x)=x^5-5x^4 in matrix form?

The only reason I ask is in case its not a taylor series for my basis.

 

[Euge]

Perfect!

I can see that this is a faster method but would it also work if I expanded the factors into polynomials and put them in matrix form in a 6x7 matrix with column 7 the f(x)=x^5-5x^4 in matrix form?

The only reason I ask is in case its not a taylor series for my basis.

Which factors? You mean the powers of $x - 1$?

I can understand if you wrote the coordinates of $f$, $f'$, and $f''$ separately as column vectors (which would give the coordinate matrices of $f$, $f'$, and $f''$ relative to your new basis). However, I don't see why you would be put them in a $6\times 7$ matrix.

 

[Logan Land]

Which factors? You mean the powers of $x - 1$?

I can understand if you wrote the coordinates of $f$, $f'$, and $f''$ separately as column vectors (which would give the coordinate matrices of $f$, $f'$, and $f''$ relative to your new basis). However, I don't see why you would be put them in a $6\times 7$ matrix.

yes the factors of (x-1)^n

as in

1 -1
0 1
0 0
0 0
0 0
0 0
for vectors (1, x-1)
and so on...

- - - Updated - - -

View attachment 3441
like this

where each column is the factor expanded into a polynomial and b is the function and them perform row reduction, would that still give the same answers?

 

[Euge]

yes the factors of (x-1)^n

as in

1 -1
0 1
0 0
0 0
0 0
0 0
for vectors (1, x-1)
and so on...

- - - Updated - - -

View attachment 3441
like this

where each column is the factor expanded into a polynomial and b is the function and them perform row reduction, would that still give the same answers?

No, you don't want to do that. Stick with the Taylor method or use the binomial theorem with the identity $x = (x - 1) + 1$ to obtain coordinate matrices for $f$, $f'$, and $f''$.