Find linear aceleration.

[Nicolas Gallardo]

Homework Statement

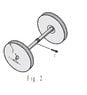
The object of the figure below has 2 disks attached on both sides through and axel of negligible mass. Both disks of mass M. I need to find the linear acceleration of this object knowing there exists a tension T on the cord.

Homework Equations

:[/B]

T=αI

The Attempt at a Solution

:[/B]

First we know that :
τ=αI ⇒
T(R-r)=I(a/R)⇒
T(R-r)=(2(MR^2)/2)(a/R)⇒
T(R-r)=MRa⇒
a=(T(R-r))/(MR)

But the solution of the exercise is : a=(T(R-r))/(3MR)

What am I doing wrong?

 

[Orodruin]

I(a/R)⇒
T(R-r)=(2(MR^2)/2)(a/R)

You are assuming that the moment of inertia relative to a point on the edge of a disk is the same as that relative to its centre. This is not true.

 

[Nicolas Gallardo]

You are assuming that the moment of inertia relative to a point on the edge of a disk is the same as that relative to its centre. This is not true.

But how would the moment of inertia change? Both of the disks are rotating with respect to the center axis...

 

[Orodruin]

Both of the disks are rotating with respect to the center axis...

No they are not, the instantaneous point of rotation is the contact point with the ground ... and you certainly are not computing the torsion relative to the central axis.

 

[Nicolas Gallardo]

No they are not, the instantaneous point of rotation is the contact point with the ground ... and you certainly are not computing the torsion relative to the central axis.

Yes! You are right! How could I be so dumb. I am sorry I am new with rigids body dinamics. Thank you for your help.