- #1
lorenz0
- 148
- 28
- Homework Statement
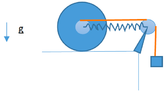
- A rope is wound around the axis orthogonal to a disk of mass ##M## and radius ##R## and there is a mass ##m## hanging from this rope as shown in the figure. The disk rests on a horizontal plane and connected to its center there is a spring which has its other second end fixed on a pulley.
(a) Determine the deformation of the spring at equilibrium.
(b) At a certain instant the mass ##m## is slightly lowered from the equilibrium position and then released. Determine the period of the oscillations that are caused by knowing that the disk rolls without slipping.
Assume ##M, R, r, k, m, m_{pulley}, r_{pulley} = r## all known.
- Relevant Equations
- ##\vec{F}=m\vec{a},\ \tau=I\alpha,\ a=R\alpha##
(a) By setting up a coordinate system with the x-axis pointing to the right and the y-axis pointing downward we have ##\begin{cases}-kx_{eq}+T_1+F_{s}=0\\ -RF_{s}+rT_1=0\\ r_p (T_2-T_1)=0\\ -T_2+mg=0\end{cases}\Rightarrow x_{eq}=\frac{mg}{k}\left(1+\frac{r}{R}\right)## which coincides with the solution given.
(b) If we denote by ##a_{D}## is the the acceleration of the center of mass of the disk, I think the the goal should then be to obtain an equation of the form ##a_{D}=\frac{\text{const}\times K}{\text{some combination of the masses}}(x-x_{eq})## so that ##T=\frac{2\pi}{\omega}## where ##\omega=\sqrt{\frac{\text{const}\times K}{\text{some combination of the masses}}}##. I have thus set up the following system:
##\begin{cases}-kx_{eq}+T_1+F_{s}=Ma_D\\ -RF_{s}+rT_1=I_D \frac{a_D}{R}\\ r_p (T_2-T_1)=I_{pulley}\alpha_{pulley}=I_{pulley}\frac{a_D}{r}\\ -T_2+mg=ma_D\end{cases}##
The problem is that the solution given says that in equation (3) the RHS should be ##\frac{I_{pulley}}{r_{pulley}}\frac{a_D}{R}(r+R)## and in equation (4) the RHS should be ##m\frac{a_D}{R}(r+R)## but I haven't been able to figure out why that is.
If the rope is ideal, shouldn't mass ##m## have the same acceleration as the disk?
Thanks
(b) If we denote by ##a_{D}## is the the acceleration of the center of mass of the disk, I think the the goal should then be to obtain an equation of the form ##a_{D}=\frac{\text{const}\times K}{\text{some combination of the masses}}(x-x_{eq})## so that ##T=\frac{2\pi}{\omega}## where ##\omega=\sqrt{\frac{\text{const}\times K}{\text{some combination of the masses}}}##. I have thus set up the following system:
##\begin{cases}-kx_{eq}+T_1+F_{s}=Ma_D\\ -RF_{s}+rT_1=I_D \frac{a_D}{R}\\ r_p (T_2-T_1)=I_{pulley}\alpha_{pulley}=I_{pulley}\frac{a_D}{r}\\ -T_2+mg=ma_D\end{cases}##
The problem is that the solution given says that in equation (3) the RHS should be ##\frac{I_{pulley}}{r_{pulley}}\frac{a_D}{R}(r+R)## and in equation (4) the RHS should be ##m\frac{a_D}{R}(r+R)## but I haven't been able to figure out why that is.
If the rope is ideal, shouldn't mass ##m## have the same acceleration as the disk?
Thanks