Find Max Volume of Cylinder Inscribed in Cone

[Chris L T521]

Thanks again to those who participated in last week's POTW! Here's this week's problem!

-----

Problem: A right circular cylinder is inscribed in a cone with height $h$ and base radius $r$. Find the largest possible volume of such a cylinder.

-----

 

[Chris L T521]

This week's question was correctly answered by Ackbach, anemone, MarkFL, and mathworker.

Here's Ackbach's solution (with graphic included by yours truly):

Spoiler

​

Let the radius of the cylinder be $s$, and its height $g$. The volume of the cylinder is then $V=\pi s^{2}g$. We will put the apex of the cone at the point $(0,h)$, and the center of the base at the origin. Then the center of the cylinder's base will also be at the origin. Consider a section of the cone with the $xy$ plane (see Figure 1). The portion of the section in the first quadrant is a straight line with equation $y=-(h/r)x+h$. Since the cylinder is inscribed, its top must intersect with this section. That is, the point $(s,g)$ must line on this line. Hence, $g=-(h/r)s+h$. Plugging this into the volume formula yields the expression
$$V=\pi s^{2} \left( - \frac{h}{r} s+h\right).$$
Here $V=V(s)$, and $h$ and $r$ are constants. We seek to maximize this function. Therefore, we take its derivative and set it equal to zero to obtain
$$V'(s)=-\frac{3 \pi h s^{2}}{r}+2 \pi h s=0 \implies s=0 \quad \text{or} \quad 2 = \frac{3 s}{r} \implies s= \frac{2r}{3}.$$
Therefore, the maximum volume is
$$V_{ \max}=V(2r/3)=\pi h (2r/3)^{2} \left(1 - \frac{2r/3}{r} \right)=\pi h \cdot \frac{4r^{2}}{27}.$$

Here's anemone's solution:

Spoiler

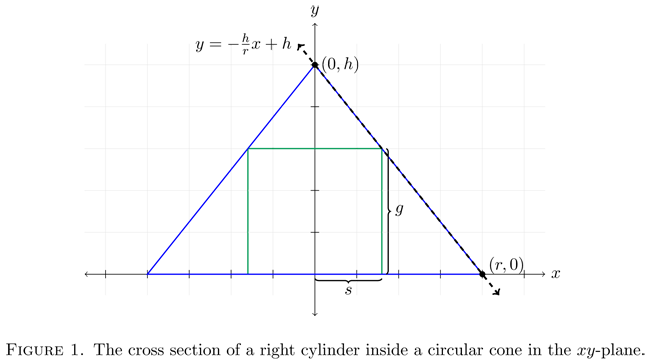
Let R and H represent the radius and height of the circular cylinder that is inscribed in a cone with height [FONT=MathJax_Math]h and base radius [FONT=MathJax_Math]r.

We know that if two triangles are similar, their corresponding side lengths are proportional. We see that the two triangles ACD and BCE are similar, hence,

$$\frac{r}{h}=\frac{R}{h-H}$$

Rearrange the equation to make H the subject (because in this problem we want to find the maximize volume of the cylinder where its formula is $$V_{\text {cylinder}}=\pi R^2h$$, it would be easier for us to make the equation of V in terms of only one variable, i.e. to get the formula of H in terms of R.):

$$r(h-H)=rR$$

$$H=\frac{h(r-R)}{r}$$

Hence,

$$V_{\text {cylinder}}=\pi R^2h=\pi R^2\left(\frac{h(r-R)}{r}\right)=\frac{\pi R^2h(r-R)}{r}$$

To find $$V_{\text{max}}$$, we find its first derivative w.r.t. R and then use the second derivative test to determine if it's a maximum value:

$$\frac{dV_{\text {cylinder}}}{dR}=\frac{d\left(\frac{\pi R^2h(r-R)}{r}\right)}{dR}=\frac{\pi Rh(2r-3R)}{r}$$; $$\frac{d^2V_{\text {cylinder}}}{dR^2}=\frac{2\pi h-6 \pi R}{r}$$

$$\frac{dV_{\text {cylinder}}}{dR}=0$$ iff $$2r-3R=0\;\rightarrow R=\frac{2r}{3}$$ $$\rightarrow \frac{d^2V_{\text {cylinder}}}{dR^2}=\frac{2\pi h-6 \pi (\frac{2r}{3})}{r}=-2\pi h (<0)$$

Hence we can conclude now that $$V_{\text{max}}=\pi R^2 h=\pi(\frac{2r}{3})^2(\frac{h(r-R)}{r})=\pi(\frac{4r^2}{9})(\frac{h(r-(\frac{2r}{3}))}{r})=\frac{4 \pi r^2h}{27}$$.