Discussion Overview
The discussion revolves around finding a point \( P \) on the line \( 3x+2y+10=0 \) that minimizes the sum of distances \( PA + PB \), where \( A \) is at \( (4,2) \) and \( B \) is at \( (2,4) \). The problem is framed within the context of optimization, potentially involving calculus techniques or geometric reasoning.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
Main Points Raised
- One participant defines the objective function \( f(x,y) \) for the distances \( PA \) and \( PB \) and seeks methods to minimize it.
- Another participant suggests that the problem is likely an optimization problem suitable for Lagrange multipliers, identifying the constraint related to the line equation.
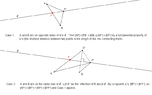
- A different participant proposes a geometric approach, discussing the reflection of point \( B \) and the intersection of lines to find point \( P \), emphasizing the shortest path principle in Euclidean geometry.
- Several participants express appreciation for the geometric method, indicating its effectiveness in solving the problem.
Areas of Agreement / Disagreement
Participants generally agree on the validity of the geometric approach to solve the problem, but there is no consensus on the preferred method, as some suggest calculus techniques while others favor geometric reasoning.
Contextual Notes
The discussion includes various assumptions about the positions of points \( A \) and \( B \) relative to the line, and the effectiveness of different methods for optimization is not fully resolved.
Who May Find This Useful
This discussion may be useful for students or individuals interested in optimization problems, particularly those involving distance minimization in geometry and calculus.