Amer
- 259
- 0
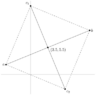
Let $a(-5,2),b(12,9)$ be two points in $\mathbb{R^2}$ find a point $c\in \mathbb{R^2}$ such that
$ac = bc$ and
$ac \perp bc$
I have a long solution I made two equations ( I considered $c (x,y)$ )
$$ ac = bc $$
$$ \sqrt{ (x +5)^2 + (y-12)^2 } = \sqrt{(x -12)^2 + ( y - 9)^2 }$$
and
$$ \frac{y-9}{x-12} \cdot \frac{y-2}{x+5} = -1 $$
and solve them by substitution
is there any faster solution shorter ?
Thanks in advance.
$ac = bc$ and
$ac \perp bc$
I have a long solution I made two equations ( I considered $c (x,y)$ )
$$ ac = bc $$
$$ \sqrt{ (x +5)^2 + (y-12)^2 } = \sqrt{(x -12)^2 + ( y - 9)^2 }$$
and
$$ \frac{y-9}{x-12} \cdot \frac{y-2}{x+5} = -1 $$
and solve them by substitution
is there any faster solution shorter ?
Thanks in advance.