Daugava
- 2
- 0
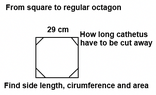
Square-shaped piece of paper is intended to make a regular octagon through the cutting of the vertices of a square.
The length of the piece of paper is 29 cm.
How long triangle cathetus have to be cut off from the vertices of the square?
Calculate the octagonal side length, circumference, and area.
Sorry for my english, if it's not understandable I'll try to explain it better.. but how do I do this?
View attachment 8187
The length of the piece of paper is 29 cm.
How long triangle cathetus have to be cut off from the vertices of the square?
Calculate the octagonal side length, circumference, and area.
Sorry for my english, if it's not understandable I'll try to explain it better.. but how do I do this?
View attachment 8187