mathlearn
- 331
- 0
Hi,
View attachment 5795
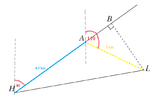
As told in the problem I drew a figure,
View attachment 5794
Next the magnitude of $$\angle BHL$$ should be found using trigonometric tables.
Can you help me to and find the angle BHL (Smile)
Many Thanks (Smile)
View attachment 5795
As told in the problem I drew a figure,
View attachment 5794
Next the magnitude of $$\angle BHL$$ should be found using trigonometric tables.
Can you help me to and find the angle BHL (Smile)
Many Thanks (Smile)
Attachments
Last edited: