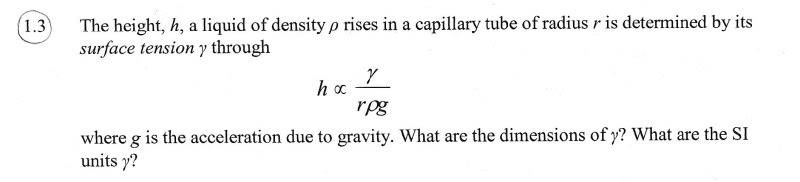SUMMARY
The discussion focuses on determining the dimensions of surface tension, specifically how to handle the directly proportional sign in the formula. The variables involved include height (h), radius (r), density (p), and gravitational acceleration (g), represented as h=(L), r=(L), p=(ML-3), and g=(LT-2). The conclusion reached is that surface tension can be expressed as M/kT2, where k is a dimensionless constant, leading to the SI units of surface tension being kg/s2.
PREREQUISITES
- Understanding of dimensional analysis in physics
- Familiarity with the concepts of direct proportionality
- Knowledge of basic fluid mechanics
- Ability to manipulate algebraic equations
NEXT STEPS
- Research dimensional analysis techniques in physics
- Learn about the principles of fluid mechanics, focusing on surface tension
- Explore the implications of dimensionless constants in physical equations
- Study the derivation of SI units for various physical quantities
USEFUL FOR
Students and professionals in physics, particularly those studying fluid dynamics, as well as anyone interested in the mathematical foundations of physical laws related to surface tension.