Find the equation of the regression line of ##x## on ##y##

[chwala]

Homework Statement

See attached.

Relevant Equations

Stats

The question is as shown below. ( Text book question).

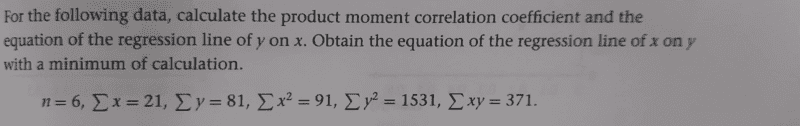
The textbook solution is indicated below.

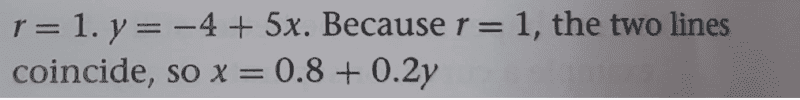Discussion;
Now they seemingly used $r=1$ to arrive at $x=0.8+0.2y$. That is,
$y=-4+5x$
then, since $r=1$, ...implying perfect correlation therefore,
$5x=4+y$
$x=0.8+0.2y$

My other way of doing this (as we we would not always have $r=1$) would be;

$\bar x=a+b\bar y$

$b=\dfrac{S_{xy}}{S_{yy}}$=$\dfrac{87.5}{437.5}=0.2$

$a=\dfrac{21}{6}-\dfrac{0.2×81}{6}=0.8$ therefore,

$x=0.8+0.2y$

Any other approach or insight is highly welcome.

 

[WWGD]

IIRC , Given a dataset $\{(x_i, y_i)\}$ , it doesn't quite workout this way. the line that minimizes the sum of squares of distances to the $\{y_i\}$ data points is not quite orthogonal to the line that minimizes the sum of squares of distances to the $\{x_i\}$ data points. Maybe @pbuk or @Stephen Tashi can verify?
Ortho projections along axes don't, afaik, work that nicely. EDIT: But there's also a "Situational" issue: Assume that calories lost , 'C'is related to hours of exercise, 'H', by the line C=200H. Does it eve make sense to say that H=C/200; that hours of exercise relates to calories used ?

 

[Office_Shredder]

This isn't asserting orthogonality, it's reflection across $x=y$. In general $\beta_x \beta_y = r^2$ so there's nothing inconsistent here between $r$ and the $\beta$s that are computed - if the correlation is perfect, the best fit lines do reflect like you want them to.

 

[WWGD]

This isn't asserting orthogonality, it's reflection across $x=y$. In general $\beta_x \beta_y = r^2$ so there's nothing inconsistent here between $r$ and the $\beta$s that are computed - if the correlation is perfect, the best fit lines do reflect like you want them to.

I was referring to the orthogonal projection from data points to the x -axis used to determine the line of best fit. It's the sum of squares of such projections that is minimized in order to determine the coefficients of the line of best fit.
Say your original line of best fit for the original data was y=mx+b and If you were to do the same when plotting x vs y instead of y vs x, your line of best fit would not be given by x=(y-b)/m, and, in particular, its slope would not be -1/m. Notice (m)(-1/m)=-1.

 

[pbuk]

The point of this question is in its last words "...with a minumum of calculation". Of course you can calculate $x = f_x(y)$ from first principals, but the point is that once you have calculated $r = 1$ and $y = f_y(x)$ you don't have to and the question is telling you not to.

@chwala you seem to be obsessed with "finding other ways to answer questions": this is often not IMHO a good thing.

 

[WWGD]

Wow, egg on my face, did not read the part of r=1 . Please ignore, apologies, I was considering a more general case for $r \neq 1$ iirc , the slope estimates will be , respectfully, $s_{xy}/s_x$ ( x on y) and $s_{xy}/s_y$ ( y on x). Edit: more here : https://stats.stackexchange.com/que...en-linear-regression-on-y-with-x-and-x-with-y

 

[chwala]

The point of this question is in its last words "...with a minumum of calculation". Of course you can calculate $x = f_x(y)$ from first principals, but the point is that once you have calculated $r = 1$ and $y = f_y(x)$ you don't have to and the question is telling you not to.

@chwala you seem to be obsessed with "finding other ways to answer questions": this is often not IMHO a good thing.

I appreciate your remarks...that's one way that has and will always help me into having an indepth understanding of math problems...cheers mate.

 

[chwala]

The point of this question is in its last words "...with a minumum of calculation". Of course you can calculate $x = f_x(y)$ from first principals, but the point is that once you have calculated $r = 1$ and $y = f_y(x)$ you don't have to and the question is telling you not to.

@chwala you seem to be obsessed with "finding other ways to answer questions": this is often not IMHO a good thing.

...just to get some insight from you...why is it not a good thing in trying to seek out other solutions or some insight on Math problems? In the best of my knowledge, I have gained immensely by doing exactly that! ...particularly on this forum. Let me know...

 

[pbuk]

...just to get some insight from you...why is it not a good thing in trying to seek out other solutions

Sometimes it is, but often it isn't. This is an example: you can solve for $y = f_y(x)$ simply by plugging numbers into an equation. Your "other solution" solves for $x = f_x(y)$ simply by plugging different numbers into the same equation - there is no insight here. However the question is asking you to look at the fact that $r = 1$ and realize that this means that you can simply solve $f_y$ for $x$ to get $f_x$.