Find the standard deviation of the values of ##y##

[chwala]

Homework Statement

See attached- sent as received both question and solution.

Relevant Equations

stats

This is the question;

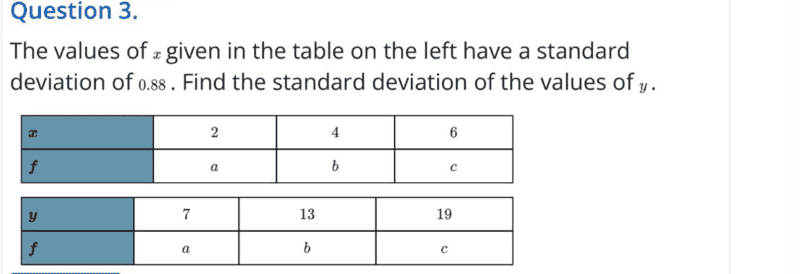This is the solution as received;

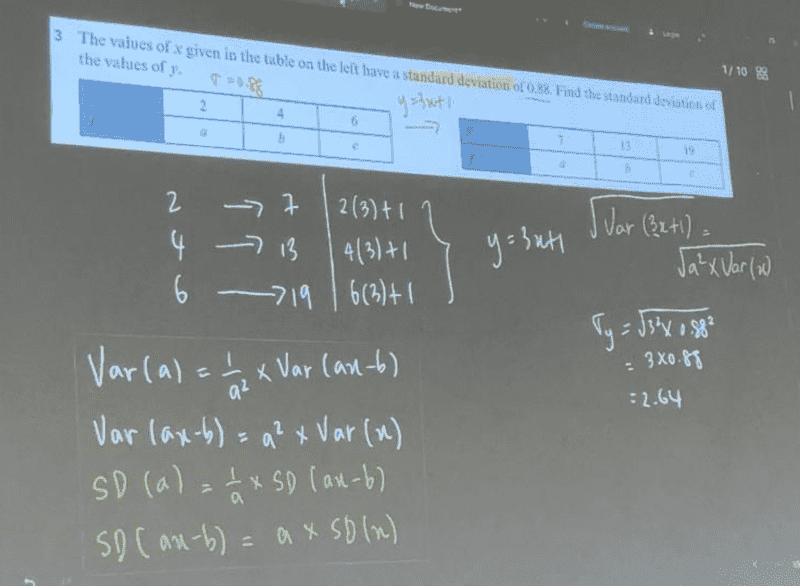
I am not familiar with the approach used in the solution...my thinking was as follows

The frequencies are the same...the only thing changing are the discrete variables thus;

Let $[x= 2,4,6]$ and $[y=7,13,19]$ form a sequence...then the nth term is given by;

$x_n=2n$ and $y_n=(3⋅2n)+1=6n+1=3(x_n)+1$

$y_n=3(x_n)+1$

I will need to think on this...your input is welcome though as we already have the solution given...not unless it is wrong. Cheers.

I will look at this later...should be achievable! Since they've given us standard deviation for $x$ ... and both frequencies have same values then I would need to find the ratio of $a:b:c$ then use that to determine the standard deviation of $y$.

 

[Mark44]

The frequencies are the same...the only thing changing are the discrete variables thus;
Let $[x= 2,4,6]$ and $[y=7,13,19]$ form a sequence...

The part about "form a sequence" doesn't make sense to me. Really, what you're talking about is a map (i.e., function) from the x values to the y values.

Let $[x= 2,4,6]$ and $[y=7,13,19]$ form a sequence...then the nth term is given by;
$x_n=2n$ and $y_n=(3⋅2n)+1=6n+1=3(x_n)+1$
$y_n=3(x_n)+1$

The last line gives the function. That is, Y = 3X + 1.

There are several properties of the variance (see https://en.wikipedia.org/wiki/Variance, in the section titled Addition and multiplication by a constant.
Among them are

• Var(X + a) = Var(X)
• Var(aX) = a²Var(X)

From these, you should be able to work out the value of Var(Y) = Var(3X + 1), and use the given value of $\sigma_X$ to find $\sigma_Y$ AKA SD(Y). Note that Var(X) = $(\sigma_X)^2$.

 

[chwala]

The part about "form a sequence" doesn't make sense to me. Really, what you're talking about is a map (i.e., function) from the x values to the y values.

The last line gives the function. That is, Y = 3X + 1.

There are several properties of the variance (see https://en.wikipedia.org/wiki/Variance, in the section titled Addition and multiplication by a constant.
Among them are×

• Var(X + a) = Var(X)
• Var(aX) = a²Var(X)

From these, you should be able to work out the value of Var(Y) = Var(3X + 1), and use the given value of $\sigma_X$ to find $\sigma_Y$ AKA SD(Y). Note that Var(X) = $(\sigma_X)^2$.

That is fine and clear ...but what happens to the $1$? all values are scaled by a constant...and i think $1$ is also a part of that constant. Should we not have;

$Var (Y)=\sqrt {a^2×Var(3x)+1}=2.82$ to two decimal places?

 

[Mark44]

Sorry, I made a typo (now corrected) in one of the formulas I wrote: It should be Var(X + a) = Var(X), not Var(a) as I originally wrote.

So if U = 3x, Var(U) = Var(3x), and so Var(U + 1) = Var(U).

Should we not have; $Var (Y)=\sqrt {a^2×Var(3x)+1}=2.82$ to two decimal places?

No, that's wrong on several counts.
$Var (Y) \ne \sqrt {a^2×Var(3x)+1}$ -- you're mixing up variance and standard deviation.
Var(Y) = Var(3X) = 3² Var(X)
So SD(Y) = $\sqrt{9 Var(X)} = 3 \sqrt{Var(X)}$

The answer given in the image you posted, 2.64, is correct. 2.82 is not.

but what happens to the 1?

It doesn't affect the calculation of the variance. A vertical translation in the data makes no difference. For example, the sets {1, 2, 3} and {3, 4, 5} have different means but the same variance, and hence the same standard deviations.