Find the tension in the rope PQ

[chwala]

Homework Statement

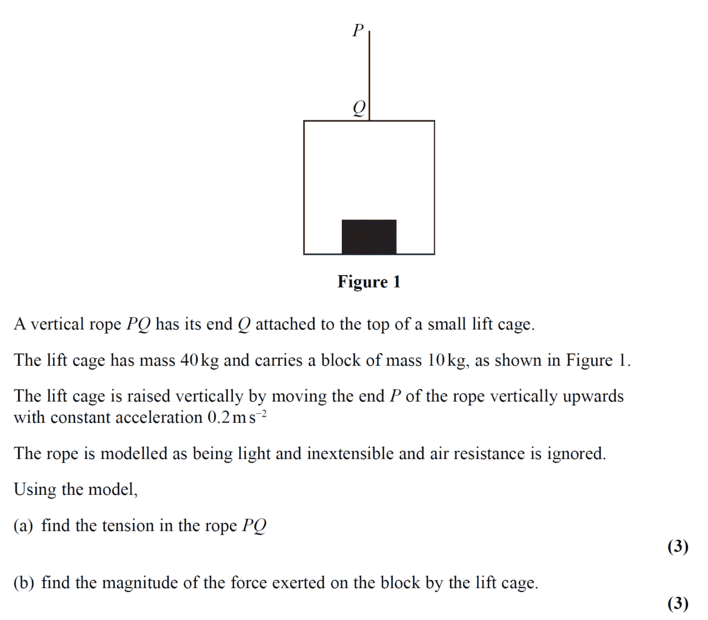
See attached.

Relevant Equations

Mechanics

My interest is on part (a), the steps are clear. I thought the final solution ought to be

$T- 500 =50 ×0.2$
$T=500+10 = 510N$


Unless I am missing something here, same query on part (b).

 

[Frabjous]

Try g=9.8m/s²

 

[chwala]

Try g=9.8m/s²

Thanks @Frabjous

 

[kuruman]

Unless I am missing something here, same query on part (b).

Does this mean that your answer for part (b) is also 510 N? If so, it is incorrect. You are missing that the rope accelerates both the cage and the block whilst the bottom of the cage accelerates only the block. That is why the two cannot be equal.

 

[chwala]

Does this mean that your answer for part (b) is also 510 N? If so, it is incorrect. You are missing that the rope accelerates both the cage and the block whilst the bottom of the cage accelerates only the block. That is why the two cannot be equal.

I used $g=10$ instead of $9.8$ Check post $3$.
Cheers.

 

[kuruman]

That would not make it correct. How about shown your answer in symbolic form?
Use
$m_c = ~$ mass of the cage
$m_b = ~$ mass of the block
$a = ~$ acceleration of cage and block
$g = ~$ acceleration of gravity
$T = ~$ the unknown tension in the rope
$F = ~$ the magnitude of the force exerted on the block by the cage.

In symbolic form the answers should be independent of the value of $g$. Once you have them, you can always substitute the numbers.

 

[Steve4Physics]

In case there is some confusion, note that using $g=9.8m/s^2$ gives the correct answer for part (a):

$M = m_c+m_b = 40+10 = 50kg$

$T - Mg = Ma$ so $T = M(g+a) = 50*(9.8+0.2) = 500N$

 

[chwala]

Does this mean that your answer for part (b) is also 510 N? If so, it is incorrect. You are missing that the rope accelerates both the cage and the block whilst the bottom of the cage accelerates only the block. That is why the two cannot be equal.

for part (a) i had using Newtons second law of motion, $F=ma$

$T-(40 +10)10 = (40+10)0.2$
$T-500=10$
$T=510N$

and in part (b) i had,
$R- 10(10)=10(0.2)$
$R=100+2=102N$

My mistake or error in using the wrong $g$ value should be clear boss. Using $9.8$ should have taken me in the right direction.