- #1
MichaelTam
- 93
- 6
- Homework Statement
- The question is comes from MIT.
- Relevant Equations
- The equation are 𝑇(𝑟+Δ𝑟)−𝑇(𝑟)=Δ𝑚𝑎𝑟, find T(r).
The whole question is:
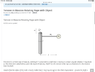
One end of a uniform rope of mass 𝑚1 and length 𝑙 is attached to a shaft that is rotating at constant angular velocity of magnitude 𝜔. The other end is attached to a point-like object of mass 𝑚2. Find 𝑇(𝑟), the tension in the rope as a function of 𝑟, the distance from the shaft.
Assume that the radius of the shaft is much smaller than 𝑙. You may also ignore the effect of gravitation - assume the shaft is rotating fast enough so that the mass and the rope are almost horizontal. Express your answer in terms of some or all of the following variables: m_1 for 𝑚1, m_2 for 𝑚2, omega for 𝜔, 𝑟 and 𝑙.
I can ‘t find the picture only website, you can find the picture at
https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/week-4-drag-forces-constraints-and-continuous-systems/problem-set-4/
My misunderstanding is the difference between l and r and the relationship in the question .
𝑟̂ :𝑇(𝑟+Δ𝑟)−𝑇(𝑟)=Δ𝑚𝑎𝑟 where 𝑎𝑟 is the radial acceleration, 𝑎𝑟=−𝜔^2𝑟 . Using that Δ𝑚=𝑚_1/(l)Δ𝑟 , the equation above becomes: 𝑇(𝑟+Δ𝑟)−𝑇(𝑟)=−Δ𝑚𝑚_1*𝑙𝜔^2𝑟. The equation set up byΔ𝑚=𝑚_1/(l)Δ𝑟 is from the tension formula. However this is the point where I don’t understand.I had separate T(r) into T_1 and T_2 , but I don’t know what is the next step?
One end of a uniform rope of mass 𝑚1 and length 𝑙 is attached to a shaft that is rotating at constant angular velocity of magnitude 𝜔. The other end is attached to a point-like object of mass 𝑚2. Find 𝑇(𝑟), the tension in the rope as a function of 𝑟, the distance from the shaft.
Assume that the radius of the shaft is much smaller than 𝑙. You may also ignore the effect of gravitation - assume the shaft is rotating fast enough so that the mass and the rope are almost horizontal. Express your answer in terms of some or all of the following variables: m_1 for 𝑚1, m_2 for 𝑚2, omega for 𝜔, 𝑟 and 𝑙.
I can ‘t find the picture only website, you can find the picture at
https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/week-4-drag-forces-constraints-and-continuous-systems/problem-set-4/
My misunderstanding is the difference between l and r and the relationship in the question .
𝑟̂ :𝑇(𝑟+Δ𝑟)−𝑇(𝑟)=Δ𝑚𝑎𝑟 where 𝑎𝑟 is the radial acceleration, 𝑎𝑟=−𝜔^2𝑟 . Using that Δ𝑚=𝑚_1/(l)Δ𝑟 , the equation above becomes: 𝑇(𝑟+Δ𝑟)−𝑇(𝑟)=−Δ𝑚𝑚_1*𝑙𝜔^2𝑟. The equation set up byΔ𝑚=𝑚_1/(l)Δ𝑟 is from the tension formula. However this is the point where I don’t understand.I had separate T(r) into T_1 and T_2 , but I don’t know what is the next step?