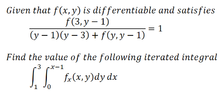SUMMARY
The discussion focuses on solving an iterated integral by changing the order of integration. Users are encouraged to present their progress to facilitate effective assistance. A specific suggestion is made to integrate the function \( f_x(x, y) \) with respect to \( x \), leading to the function \( f(x, y) \). This approach is essential for obtaining the exact form of the integral value.
PREREQUISITES
- Understanding of iterated integrals
- Knowledge of changing the order of integration
- Familiarity with functions of multiple variables
- Basic calculus concepts, including integration techniques
NEXT STEPS
- Study techniques for changing the order of integration in double integrals
- Learn about the properties of functions of multiple variables
- Practice solving iterated integrals with different functions
- Explore advanced integration techniques, such as Fubini's Theorem
USEFUL FOR
Students and educators in calculus, mathematicians working with multivariable functions, and anyone seeking to improve their skills in solving iterated integrals.