Find the volume of th eresulting solid by and method

[tony873004]

The region bounded by the curves is rotated about the specified axis. Find the volume of th eresulting solid by and method.

x^2 + \left( {y - 1} \right)^2 = 1

First question want it rotated about the x-axis, the second question wants it rotated about the y-axis.

So I re-write it in terms of x. Seems easier than in terms of y since there's only 1 x term.
x = \sqrt { - y^2 + 2y} <br />


The problem is when I graph it,

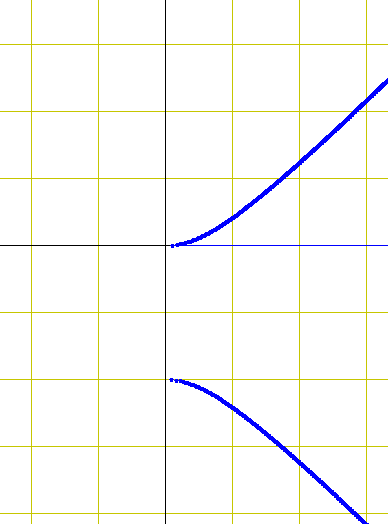
So nothing is bounded. There is no solid to rotate. Should I have solved in terms of y instead? How would I do that?

 

[cepheid]

Don't you need to take both the positive and negative square roots?

 

[tony873004]

Don't you need to take both the positive and negative square roots?

Thanks for your reply.

It still seems like there is no bounded region. All the other problems in this section give a second curve, usually a line like y=2, just to bound the curve. What am I doing wrong? Did I properly solve for x?

 

[HallsofIvy]

You have lost a "sign". x²+ (y-1)²= 1 is obviously a circle of radius 1 with center at (0, 1), not the hyperbola you show.

x= \pm \sqrt{1-(y-1)^2}= \pm \sqrt{2y- y^2}
and
y= 1\pm \sqrt{1- x^2}

 

[tony873004]

lol... and I should have recognized that the answer in the back of the book, 4pi/3 is the volume of a unit sphere. Without the r^3 in the formula I didn't recognize it.

Thanks, Halls