- #1
Adesh
- 735
- 191
- Homework Statement
- Find the volume when three cylinders of radius 1 intersect orthogonally.
- Relevant Equations
- Volume = area x height
I know that to find the volume under a surface and above a boundary we have to integrate twice. I can explain myself with an example :-
Lets' consider that we need to find the volume under the surface [itex] z = \sqrt{1-x^2} [/itex] and above the region bounded by [itex] y^2 = x [/itex] and positive x-axis and [itex] x=5 [/itex] . So, what I would do is to first define the limits of x and y , so [itex] -\sqrt{x} < y < \sqrt{x} [/itex] and for x we have [itex] 0 < x < 5 [/itex] so we can now carry out our integrals like this [itex] \int_ {-\sqrt{x}}^{\sqrt{x}} \sqrt{1-x^2} dy [/itex] which I can call [itex] A(x) [/itex] and then I can integrate [itex] A(x) [/itex] from [itex] 0 to 5 [/itex] and hence I will get the desired volume.
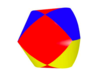
But when it comes to three intersecting cylinders I can't figure out under what and above what I have to find the volume . I have added an attachment which shows the solid that we get after intersection, but I still can not figure out how to go on? Can anybody please help to indemnify the upper and lower surfaces? Is it that my knowledge (that dividing the lower surface into small vanishing rectangles and calculating the volume of rectangular columns and then summing it up) is inadequate for this problem?
I must confess that there are lot of solutions available for the Computation of Volume under three Intersecting Cylinders on google search but it's also true that all of them do it by symmetry which also is not understandable by me due to lack of visualization . I resp[ect this site therefore I have asked here.
THANK YOU, ANYHELP HELP WILL BE MUCH APPRECIATED.
Lets' consider that we need to find the volume under the surface [itex] z = \sqrt{1-x^2} [/itex] and above the region bounded by [itex] y^2 = x [/itex] and positive x-axis and [itex] x=5 [/itex] . So, what I would do is to first define the limits of x and y , so [itex] -\sqrt{x} < y < \sqrt{x} [/itex] and for x we have [itex] 0 < x < 5 [/itex] so we can now carry out our integrals like this [itex] \int_ {-\sqrt{x}}^{\sqrt{x}} \sqrt{1-x^2} dy [/itex] which I can call [itex] A(x) [/itex] and then I can integrate [itex] A(x) [/itex] from [itex] 0 to 5 [/itex] and hence I will get the desired volume.
But when it comes to three intersecting cylinders I can't figure out under what and above what I have to find the volume . I have added an attachment which shows the solid that we get after intersection, but I still can not figure out how to go on? Can anybody please help to indemnify the upper and lower surfaces? Is it that my knowledge (that dividing the lower surface into small vanishing rectangles and calculating the volume of rectangular columns and then summing it up) is inadequate for this problem?
I must confess that there are lot of solutions available for the Computation of Volume under three Intersecting Cylinders on google search but it's also true that all of them do it by symmetry which also is not understandable by me due to lack of visualization . I resp[ect this site therefore I have asked here.
THANK YOU, ANYHELP HELP WILL BE MUCH APPRECIATED.