MHB Find unknown angles of a triangle

  • Thread starter Thread starter tantrik
  • Start date Start date
  • Tags Tags
    Angles Triangle
AI Thread Summary
The discussion revolves around calculating unknown angles in a triangle with given sides and an exterior angle. The user has established that angle ADC is 72 degrees and that the sum of angles BAD and BCD equals 108 degrees. There is uncertainty regarding the properties of the triangle, particularly whether it is isosceles or equilateral, which affects the calculations. Participants suggest using the sine law and clarify that triangle BCD is an isosceles right triangle, leading to angles BDC and CDB being 45 degrees. The conversation highlights the need for precise problem statements and the importance of understanding triangle properties for accurate angle calculations.
tantrik
Messages
13
Reaction score
0
Dear friends,

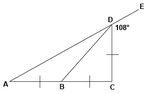
I am unable to find out the unknown angles for the following triangle which I attached with this post.

View attachment 6092

Angle BAD and angle BCD are the unknown angles need to be calculated. Given that lines AB=BC=CD and angle CDE = 108 degrees

From my calculations: angle ADC = 180 - 108 = 72 degrees (angles on a straight line)

angle BAD + angle BCD = 108 degrees (exterior angle of a triangle = sum of interior opposite angles)

I could not proceed any further beyond this. I thought line DB (median) is bisecting angle ADC since line DB is bisecting line AC (AB=BC) but this only happens in case of isosceles and equilateral triangles.

I am very much stuck here and seek your kind suggestions here. I am also suspecting something could be wrong in the diagram of the triangle or may be the unknown angles. Let me know where I am wrong. Thanks in advance.
 

Attachments

  • Math pic.jpg
    Math pic.jpg
    4 KB · Views: 142
Mathematics news on Phys.org
Without a loss of generality, let the equal segments be equal to 1 unit each and then apply the sine law.
 
greg1313 said:
Without a loss of generality, let the equal segments be equal to 1 unit each and then apply the sine law.

Thanks but is it possible to solve this question just by using geometry principles?
 
Can you post the exact problem statement? (I'm assuming you're giving us your version of it). Where did you get the problem?
 
greg1313 said:
Can you post the exact problem statement? (I'm assuming you're giving us your version of it). Where did you get the problem?

No, this exactly how the question (diagram only, no other info about triangles or angles) has been provided by the math teacher in the school.
 
Use the fact that, since triangle BCD is an isosceles right triangle, angles BDC and CDB have measure 45 degrees.

The rest is easy.
 
HallsofIvy said:
Use the fact that, since triangle BCD is an isosceles right triangle, angles BDC and CDB have measure 45 degrees.

The rest is easy.

It's not a right-angled triangle. If it were, arctan(1/2) would be 18 degrees but arctan(1/2) is about 27 degrees.
 

Similar threads

MHB Difference of angles in a triangle
Replies
4
Views
1K
B A triangle problem: Prove that |AC|+|AB|=|PR|+|PQ| given some constraints
Replies
13
Views
2K
MHB What are the angles of an isosceles triangle with a specific ratio?
Replies
2
Views
1K
MHB Can You Find the Angle in This Isosceles Triangle Problem?
Replies
1
Views
1K
MHB Find Length of Side in Right Triangle w/ 45°, 90°, and 45° Angle
Replies
2
Views
2K
MHB Acute angle of right triangles
Replies
4
Views
1K
dissecting an isosceles triangle
Replies
2
Views
2K
MHB Prove Equal Area Triangle & Parallelogram, $\angle ADC=90^{\circ}$
Replies
9
Views
3K
MHB Finding a particular angle withion Johnson Solid J2
Replies
2
Views
2K
MHB Solve for the angles in a triangle
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top