Finding area of a non right angled triangle

[Eobardrush]

Homework Statement

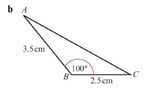
Find the area of this triangle

Relevant Equations

0.5 x a x c x Sin B

I just simply used the formula to solve. Note the "x" represents multiplication in this case

0.5 x a x c Sin B

This is based on the conditions given in the textbook I am using which quotes "Use this formula to find the area of any triangle when you know 2 sides and an angle between them"

So I got my answer as follows: 0.5 x 3.5 x 2.5 x Sin 100 = 4.31 cm²

It is correct but what I am struggling is in understanding how I can do this without relying on the formula, like splitting this into a right angled triangle(by finding height for example)
I attached a diagram I drew about this triangle. As you can see I tried to split this into a right angled triangle

Can someone give me some insights on how I can try to find this without relying on the formula so that I would better understand how this works?

Note that I did see the proof of the formula but it was for the normal looking triangles(with acute angles) so I am not sure how to apply the proof to this type of triangle

 

[FactChecker]

Suppose that $a$ is the length of the base. Then $c \sin(B)$ is simply the height perpendicular to the base. So the equation that you gave as the Relevant Equation really is $area = 0.5 * base * height$.

 

[jbriggs444]

Homework Statement:: Find the area of this triangle
Relevant Equations:: 0.5 x a x c x Sin B

Can someone give me some insights on how I can try to find this without relying on the formula so that I would better understand how this works?

Imagine the triangle as a bunch of thin horizontal slices, stacked up vertically. Obviously, the stack here is slanted to the left.

Now slide all of the slices to the right so that their left edges line up. Obviously this does not change the total area. And obviously the result is a right triangle.

 

[Prof B]

As you can see I tried to split this into a right angled triangle

I can't tell from your picture, but assume that the leftmost point in the triangle is A and the rightmost point is C.

The line segment that you labeled h is not an altitude in ABC.

Draw the line containing BC. Draw a line through A perpendicular to the line containing BC. Say it intersects that line at X. Then AX is the altitude to BC in the triangle ABC. From the picture you will see that $\triangle ABC = \triangle AXC - \triangle AXB$

 

[Eobardrush]

I can't tell from your picture, but assume that the leftmost point in the triangle is A and the rightmost point is C.

The line segment that you labeled h is not an altitude in ABC.

Draw the line containing BC. Draw a line through A perpendicular to the line containing BC. Say it intersects that line at X. Then AX is the altitude to BC in the triangle ABC. From the picture you will see that $\triangle ABC = \triangle AXC - \triangle AXB$

Thank you! I was able to do it, although it was pretty long. Sorry if the workings look unclear. Was wondering since it was pretty long if there is a shorter way of doing this?(Excluding using the formula I mentioned)
I mean like I might have used some extra unnecessary steps here
Any steps that I should exclude in my workings here?

 

[FactChecker]

Was wondering since it was pretty long if there is a shorter way of doing this?

As @jbriggs444 said in post #3, you can see that the top of the original triangle can get slid to the right, making a right triangle, without changing the area. That gives you a simpler $area = 1/2 * base * height$ for a right triangle without worrying about the other triangle with $b$.

(Excluding using the formula I mentioned)
Or is this the shortest method there is

You will still need to use the $area = 1/2 * base * height$ equation for a right triangle, but that is so simply related to the $base * height$ formula for the rectangle that it is practically intuitive.

 

[Eobardrush]

As @jbriggs444 said in post #3, you can see that the top of the original triangle can get slid to the right, making a right triangle, without changing the area. That gives you a simpler $area = 1/2 * base * height$ for a right triangle without worrying about the other triangle with $b$.

I am really bad at visualizing things so I was not able to visualize what he said

 

[FactChecker]

I am really bad at visualizing things so I was not able to visualize what he said

Take a deck of cards with $area = deckBase * deckHeight$. Now slide the top slightly to the left until the left edge is tilted like your triangle. Clearly, the stack of cards still has the same $area = deckBase * deckHeight$ as the original deck. Half of that is your triangle area.

 

[vela]

I was able to do it, although it was pretty long. Sorry if the workings look unclear. Was wondering since it was pretty long if there is a shorter way of doing this?(Excluding using the formula I mentioned)

I'd suggest you recalibrate your sense of what a long problem is. :)

One way of reducing the number of calculations would be to not use numbers until the end.
\begin{align*}
\triangle AXC &= \frac 12 h (b+c) \\
\triangle AXB &= \frac 12 h b \\
\triangle ABC &= \triangle AXC - \triangle AXB = \frac 12 h (b+c) - \frac 12 h b = \frac 12 h c
\end{align*} Note that this eliminates the need to find the length $b$ because it cancels out in the end. Use trig to find $h$, and you've essentially derived the formula you used in the beginning, but now you can see why it works.

 

[Prof B]

Note that I did see the proof of the formula but it was for the normal looking triangles(with acute angles) so I am not sure how to apply the proof to this type of triangle

It is good that you are interested in this sort of thing. Note that in the case that X is between A and B it is not necessary to calculate |AX| or |BX|. That sort of observation is helpful when you try to work out other cases yourself.