I got the summation this way:
In n=j+2k+3m, write the number n as a bunch of circles from left to right. Consider the entire number "filled up" by 1's, one 1 to a circle. This is 1 possible sum, corresponding to j = n, k = 0, m = 0. Then starting at the left, group 2 circles together. This is another possible sum, corresponding to j = n-2, k = 1, m = 0. Then group another two circles from the left, corresponding to j = n-4, k = 2, m = 0. It can be seen from this that the number of ways to form n using only 1's and 2's is floor(n/2) + 1.
Then deal with 3's. For each amount of threes you use (say there are i threes) you have n - 3i left to form using only 1's and 2's. And you can have 0, 1, ..., floor(n/3) threes. From this I get the summation.
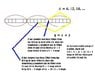
Also, if your equation is correct then my quadratic is also correct for all n divisible by 6. How I got the quadratic is interesting. Consider a group of 6 units when n is written out like I said earlier (in unary). This group is either the rightmost group, or there are 6 units between it and the right, or 12, so on up to n-6 units to the right of it. Now say that the entire number to the left of that group has been filled up by 3's, and the left half of the group is also covered by a 3, and that there are no threes to the right of that group. Given that, the question is, how many ways are there to fill the as-yet-unfilled part of the number with 1's, 2's, and 3's? (see attachment)
So sum up the groups of 6: E(i = 0 to n/6) (6i/2 + 1 + (6i + 2) / 2 + 1). But this is an overcount, because when i = n/6, x = n and y = n + 3 in the diagram. x = n is a case you do want to count, but y = n + 3 is the case when n has been filled from the left by "negative one" threes. So subtract (n + 2) / 2 + 1 back out, for (E(i = 0 to n/6) (6i/2 + 1 + (6i + 2) / 2 + 1)) - ((n + 2) / 2 + 1). This simplifies to n^2 / 12 + n / 2 + 1.