SUMMARY
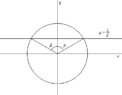
The discussion focuses on finding the coordinates for the equation sin(2x) = 1/2, specifically identifying the point P. The correct coordinates are established as (17π/12, 1/2). The periodicity of the sine function is utilized, with the period of sin(2x) being π. The general solution for sin(θ) = 1/2 is derived, leading to the conclusion that the value of x can be expressed as x = 17π/12.
PREREQUISITES
- Understanding of trigonometric functions and their properties
- Knowledge of periodicity in trigonometric equations
- Familiarity with solving equations involving sine
- Ability to manipulate and solve inequalities
NEXT STEPS
- Study the periodic properties of trigonometric functions
- Learn about the unit circle and its application in solving trigonometric equations
- Explore the concept of general solutions for trigonometric equations
- Investigate the graphical representation of sine functions and their intersections
USEFUL FOR
Students and educators in mathematics, particularly those focusing on trigonometry, as well as anyone looking to deepen their understanding of solving trigonometric equations and their graphical interpretations.