Finding moments in pedal (beam w/ rightangles)

  • Thread starter Thread starter Letsgetphysicscool
  • Start date Start date
  • Tags Tags
    Moments Pedal
Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
Sign up Log in
7 replies · 2K views
Letsgetphysicscool
Messages
4
Reaction score
0
hello friends i am seek advice on a engineer question (sorry if grammar bad english isn't my first language but i learn)

i require to find the moments on a pedal. the pedal is horizonta. as the picture provided the hinge point is at a and there is a support at b. at e a man stands and is 750 Newton and dimension ab = 375 bc=140 cd=150 de=380 ef=70. all angles are 90 degrees.
bitmap.png


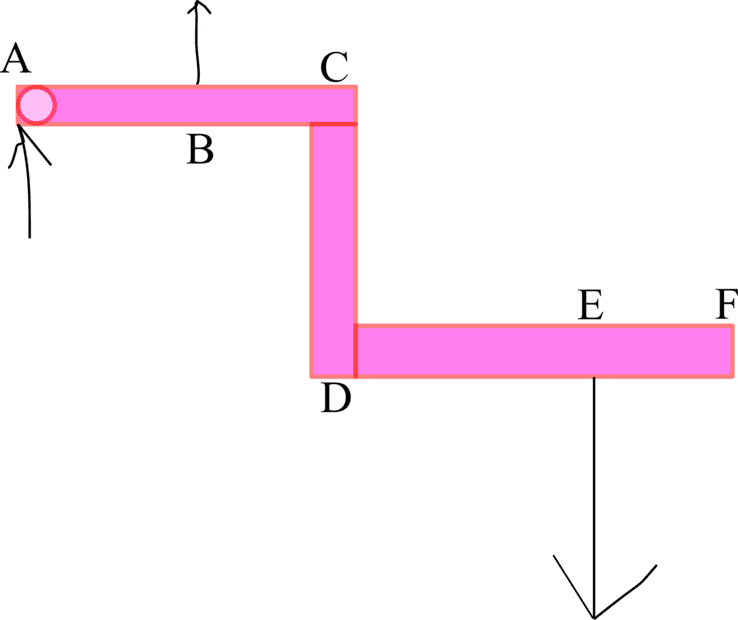
i know how resolve if it had no vertical on beam but vertical at cd is confuse. what is the best way to tackle this problem? i wish for speedy conclusion i want to learn not be told answer
what i know is i have clockwise moment across the beam because a is hinge point so forces to resolve on rightward side

do i structure the problem in three parts with diagrammes follow?
then calculate the vertical reaction forces on a and b i am only to consider the dimensions of abc and def and the dimension cd is a mislead?

thank kindly
 
Last edited:

Discussion

Physics news on Phys.org
Welcome to PF. :smile:

Yes, you need to finish the FBD that you've started above. Note that the force you show at the hinge point A is opposite to the direction I would expect for countering the torque due to the person standing on the structure.

Also, is this for schoolwork? If so, we can move it to the schoolwork forums for you.
 
berkeman said:
Welcome to PF. :smile:

Yes, you need to finish the FBD that you've started above. Note that the force you show at the hinge point A is opposite to the direction I would expect for countering the torque due to the person standing on the structure.

Also, is this for schoolwork? If so, we can move it to the schoolwork forums for you.
thank you friend. i replaced the diagramme for a newer one.

so calculate the vertical reaction forces on a and b i only consider the dimensions of abc and def (vertical on the beam) and not cd (horizontal on the beam)?
 
Is the support at B a spring?
Does the force at E remain perpendicular to the structure as it rotates?
E to F need not be considered if the downward force is concentrated at E.
 
AZFIREBALL said:
Is the support at B a spring?
Does the force at E remain perpendicular to the structure as it rotates?
E to F need not be considered if the downward force is concentrated at E.
thank you friend

b is not spring is a rope support from above beam not coming from below. and the beam with the hinge point a and load at point e it is in equalibrium. e is point load yes is perpendicular
 
Last edited:
berkeman said:
Also, is this for schoolwork? If so, we can move it to the schoolwork forums for you.
@Letsgetphysicscool -- I don't think you've answered this question of mine yet...
 
And whether it is a schoolwork assignment or not, can you show us your sum of forces and sum of moments equations from the FBD? It's better if you use LaTeX to post the math equations instead of trying to fit them into ASCII simplifications (see the LaTeX Guide link below the Edit window). Thanks. :smile:
 
berkeman said:
And whether it is a schoolwork assignment or not, can you show us your sum of forces and sum of moments equations from the FBD? It's better if you use LaTeX to post the math equations instead of trying to fit them into ASCII simplifications (see the LaTeX Guide link below the Edit window). Thanks. :smile:
hello friend

this is what i stuck with and i say in first message. i confuse with vertical part on beam at cd otherwise i can do.

i don't know how to account for vertical part on horizontal.

is there general formula or rule? once i know this i can resolve for a and b