Finding the angle opposite the R

  • MHB
  • Thread starter Drain Brain
  • Start date
  • Tags
    Angle
In summary, to find the angle opposite the R in a triangle, you can use the Law of Sines or the Law of Cosines. Knowing this angle is important in solving various triangle problems and applications of trigonometry. A calculator can be used to find this angle, and it can be labeled as "R", "∠R", or "θ". Special cases include right triangles and equilateral triangles.
  • #1
Drain Brain
144
0
can you show me another way of finding the angle opposite the resultant

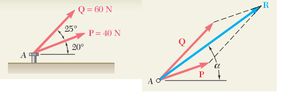
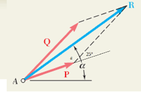
the way I find it is by constructing a parallelogram and knowing that the angles in a parallelogram add up to 360 deg and knowing that the angle between F1 and F2 is 25 deg then I subtracted twice of that to 360 deg getting 310 deg and dividing by 2 I get the angle opposite R as 155 deg.

can you show me another method on how to determine that without using parallelogram rule. thanks!
 

Attachments

  • MEch.png
    MEch.png
    4.1 KB · Views: 81
Mathematics news on Phys.org
  • #2
We may use the following:

View attachment 2820

\(\displaystyle a+25^{\circ}=180^{\circ}\)

\(\displaystyle a=155^{\circ}\)
 

Attachments

  • drainbrain.png
    drainbrain.png
    8.7 KB · Views: 71

FAQ: Finding the angle opposite the R

How do I find the angle opposite the R in a triangle?

The angle opposite the R in a triangle is also known as the opposite angle or opposite side angle. To find this angle, you can use the Law of Sines or the Law of Cosines. The Law of Sines states that the ratio of a side length to the sine of its opposite angle is constant, while the Law of Cosines relates the lengths of the sides of a triangle to the cosine of one of its angles.

What is the importance of finding the angle opposite the R?

Knowing the angle opposite the R is important in solving various problems involving triangles, such as finding the missing side length or angle measure. It is also crucial in applications of trigonometry, such as in navigation, engineering, and physics.

Can I use a calculator to find the angle opposite the R?

Yes, you can use a calculator to find the angle opposite the R. Most scientific or graphing calculators have built-in functions for solving trigonometric equations. Make sure to input the correct values for the sides and angles in order to get an accurate result.

How do I label the angle opposite the R in a triangle?

The angle opposite the R can be labeled as simply "R", "∠R", or "θ", depending on the context or preference. It is usually labeled with a letter or symbol that corresponds to the vertex opposite the angle. For example, if the angle is opposite to vertex A, it can be labeled as "A" or "∠A".

Are there any special cases when finding the angle opposite the R?

Yes, there are special cases when finding the angle opposite the R. If the triangle is a right triangle, the angle opposite the hypotenuse (the longest side) is always 90 degrees. Additionally, if the triangle is an equilateral triangle, all three angles are equal and therefore the angle opposite the R is also equal to the other two angles.

Similar threads

MHB Left or Right Angles ( + or - ) of adjoining vectors
Replies
2
Views
1K
Calculating distance of Mars from the Sun based on two elongations
Replies
2
Views
996
Engineering Resultant Force and Direction using Parallelogram Law
Replies
6
Views
2K
MHB Finding the Resultant Angle for Vector Addition Using Law of Sines and Cosines
Replies
4
Views
2K
MHB Find the sin angle between two 2d vectors
Replies
1
Views
1K
MHB Find unknown angles of a triangle
Replies
6
Views
3K
MHB Find the areas of segment in circle
Replies
1
Views
2K
MHB Find Angles of Spherical Triangle $\mathcal{P}$
Replies
1
Views
1K
MHB Finding the Leg Lengths of a Right Triangle with an Acute Angle of 22°
Replies
2
Views
1K
A How Does U(1) Double-Cover SO(2) for a Specified Angle?
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top